Núcleo Temático 2 Princípios Básicos de Probabilidades

En este Núcleo Temático se definen algunos conceptos que servirán de soporte para comprender el concepto de probabilidad. Para ello, en la primera sección, se hace una introducción a los conjuntos, lo cual es necesario para entender la definición clásica de la probabilidad. Luego, en la segunda sección, se definen algunas operaciones con conjuntos. Por último, la tercera sección, constituye una introducción a la probabilidad.

El siguiente bloque de código permite instalar y cargar los paquetes de R que se usaran en esta sección.

packages <- c(
  "ggplot2", "ggstatsplot",
  "ggVennDiagram", "eulerr",
  "latex2exp", "venneuler",
  "VennDiagram", "RColorBrewer"
)
package.check <- lapply(packages, FUN = function(x) {
  if (!require(x, character.only = TRUE)) {
    install.packages(x, dependencies = TRUE)
    library(x, character.only = TRUE)
  }
})

2.1 Introducción a los Conjuntos

En esta sección se definen algunos conceptos relacionados a la teoría de conjuntos. Estos conceptos son necesarios para entender el enfoque clásico de la probabilidad, el cual se describe en la sección 2.3.4.1.

2.1.1 Conjunto

Definición 2.1 (Conjunto) Un conjunto es una colección bien definida de objetos, los cuales se denominan elementos o miembros del conjunto. Generalmente se utilizan letras mayúsculas, como \(A\), \(B\), \(X\), \(Y\), \(\dotsc\) para designar los conjuntos, y letras minúsculas, como \(a\), \(b\), \(x\), \(y\), \(\dotsc\) para designar los elementos de los conjuntos. Las palabras clase, colección y familia son sinónimos de conjunto.

Para decir que un elemento \(a\) pertenece a un conjunto \(A\) se escribe \(a \in A\). (Donde el símbolo \(\in\) significa “es un elemento de”). También se escribe \(a,b \in A\) cuando \(a\) y \(b\) pertenecen a A.

2.1.1.1 Formulación de Conjuntos por Extensión

Definición 2.2 (Formulación de Conjuntos por Extensión) Consiste en formular el conjunto listando todos los elementos del conjunto. Por ejemplo,

\[A=\left\{1,2,3 ,5,7,9\right\}\]

significa que \(A\) es el conjunto que comprende los números \(1, 2, 3 ,5, 7 \:y\: 9\). Observe que los elementos del conjunto están separados por comas y encerrados en corchetes\(\{\:\:\}\).

2.1.1.2 Formulación de Conjuntos por Comprensión

Definición 2.3 (Formulación de Conjuntos por Comprensión) Consiste en formular el conjunto a través de propiedades que caracterizan los elementos en el conjunto, es decir, las propiedades que tienen los miembros del conjunto y que no tienen los no miembros. Por ejemplo:

\[A=\left\{x:x \:es\: \:un\: número\: impar, \,x<10\right\}.\]

En muchos casos es inviable formular un conjunto por extensión, en tal caso se hace necesario formularlo por comprensión.

2.1.1.3 Tamaño de un Conjunto

Definición 2.4 (Tamaño de un Conjunto) El tamaño de un conjunto \(S\) (también, cardinalidad o cardinal del conjunto) es el número de elementos del conjunto y se denota por \(n(S)\). El tamaño del conjunto vacío es cero, es decir, \(n(\emptyset)=0\).

2.1.1.4 Conjunto Finito

Definición 2.5 (Conjunto Finito) Un conjunto \(S\) es finito si \(S\) es vacío o si el tamaño de \(S\) es exactamente un número \(m\) entero positivo \(\left(n(S) = m \in \mathbb{ N } \right)\); de otra manera es infinito.

2.1.1.5 Conjunto Contable

Definición 2.6 (Conjunto Contable) Un conjunto \(S\) es contable si \(S\) es finito o si los elementos de \(S\) pueden ser colocados en forma de sucesión, en cuyo caso se dice que \(S\) es infinito contable. Un conjunto es incontable si este no es contable.

Considere los siguientes ejemplos:

1. Sea \(A\) el conjunto de las letras del alfabeto y sea \(D\) los días de la semana, es decir, \(A=\left\{a,b,\dotsc,y,z\right\}\) y \(D=\left\{lunes,martes,\dotsc,domingo \right\}\). Entonces \(A\) y \(D\) son conjuntos finitos. Específicamente el tamaño de \(A\) es 27 \(\left(n(A)=27 \right)\) y el tamaño de \(D\) es 7 \(\left(n(D)=7\right)\).

2. Sea \(R=\left\{x:x \textit{ es un río de la tierra} \right\}\). Aunque puede ser difícil contar el número de ríos sobre la tierra, \(R\) continúa siendo un conjunto finito.

3. Sea \(E\) el conjunto de los enteros positivos pares y sea \(I\) el intervalo unidad; es decir, \(E=\left\{2,4,6,\dotsc\right\}\) e \(I=[0,1]=\left\{x:0≤x≤1\right\}\). Entonces, ambos conjuntos son infinitos. De manera particular \(E\) es infinito contable e \(I\) es infinito incontable.

2.1.2 Subconjunto

Definición 2.7 (Subconjunto) Sean \(A\), \(B\) dos conjuntos; se dice que \(A\) es un subconjunto de \(B\), o se dice también que \(A\) está contenido en \(B\), si todos los elemento del conjunto \(A\) también pertenecen al conjunto \(B\), y se escribe como \(A \subseteq B\) o \(B \supseteq A\).

La afirmación \(A \subseteq B\) no excluye la posibilidad de que \(A=B\). Sin embargo, si \(A \subseteq B\) y \(A\neq B\), entonces se dice que \(A\) es un subconjunto propio de \(B\) (escrito algunas veces \(A \subset B\)).

2.1.3 Conjuntos Iguales

Definición 2.8 (Conjunto Iguales) Dos conjuntos \(A\), \(B\) son iguales si ambos contienen exactamente los mismos elementos o, en forma equivalente, si cada uno está contenido en el otro. Es decir, \(A = B\) si y sólo si \(A \subseteq B\) y \(B \supseteq A\). Esto implica que si cualquier elemento \(a \in A\), entonces \(a \in B\).

Las negaciones de \(a \in A, A \subseteq B, B \supseteq A, \:y\: A=B\) se escriben \(a \notin A\), \(A \nsubseteq B, B \nsupseteq A, \:y\: A \neq B\).

Teorema 2.1 Sean \(A\), \(B\), \(C\) cualquier conjunto. Entonces:

1. \(A \subseteq A\)
2. Si \(A \subseteq B\) y \(B \supseteq A\), entonces \(A=B\)
3. Si \(A \subseteq B\) y \(B \subseteq C\), entonces \(A \subseteq C\).

2.1.4 Conjunto Universal

Definición 2.9 (Conjunto Universal) Es cualquier conjunto \(\mathbb{U}\) que contiene a todos los conjuntos bajo investigación en cualquier aplicación de una teoría de conjuntos. Por ejemplo en geometría de planos, el conjunto universal comprende todos los puntos en el plano; en los estudios de población humana, el conjunto universal consiste de todas las personas del mundo.

2.1.5 Conjunto Vacío o Conjunto Nulo

Definición 2.10 (Conjunto Vacío) Un conjunto vacío es aquel que no tiene elementos y se representa por \(\emptyset\).

Por ejemplo, el conjunto \(S=\left\{x:x \textit{ es un entero positivo},x^2=3 \right\}\) es un conjunto vacío, puesto que ningún entero positivo tiene la propiedad requerida.

Teorema 2.2 Para cualquier conjunto \(A\), se tiene \(\emptyset \subseteq A \subseteq \mathbb{U}\).

2.1.6 Conjuntos Disyuntos o Mutuamente Excluyentes o Ajenos

Definición 2.11 (Conjuntos Disyuntos o Mutuamente Excluyentes o Ajenos) Se dice que dos conjuntos \(A\), \(B\) son disyuntos si estos no tienen elementos en común.

Consideremos, por ejemplo, los conjuntos \[A=\left\{1,2\right\}; B=\left\{2,4,6\right\}; C=\left\{4,5,6,7\right\}.\] Observe que \(A\) y \(B\) no son disyuntos porque cada uno tiene el elemento 2, y \(B\) y \(C\) no son disyuntos puesto que cada uno contiene el elemento 4, entre otros. Por otra parte, \(A\) y \(C\) son disyuntos dado que estos no tienen elementos en común. Se observa que si dos conjuntos son disyuntos, entonces ninguno es subconjunto del otro (a menos que uno sea el conjunto vacío).

2.1.7 Conjunto Solapados o Traslapados

Definición 2.11 (Conjunto Solapados o Traslapados) Se dice que dos conjuntos \(A\), \(B\) son solapados si estos tienen por lo menos un elemento en común.

Consideremos, por ejemplo, los conjuntos \[A=\left\{1,2\right\}; B=\left\{2,4,6\right\}; C=\left\{4,5,6,7\right\}.\] Observe que \(A\) y \(B\) son solapados porque cada uno tiene el elemento 2, y \(B\) y \(C\) son solapados puesto que cada uno contiene el elemento 4, entre otros.

2.1.8 Diagrama de Venn

Definición 2.12 (Diagrama de Venn) Un diagrama de Venn es una representación en dibujo de conjuntos, donde estos están representados por áreas encerradas en el plano. El conjunto universal \(\mathbb{U}\) está representado por los puntos en un rectángulo y los demás conjuntos están representados por círculos, elipses o óvalos, generalmente; que se encuentran dentro de los rectángulos.

La figura 2.1 ilustra por medio de diagramas de Venn diferentes relaciones entre los conjuntos \(A\) y \(B\).

knitr::include_graphics(path = "figuras/diagrama_venn.png")

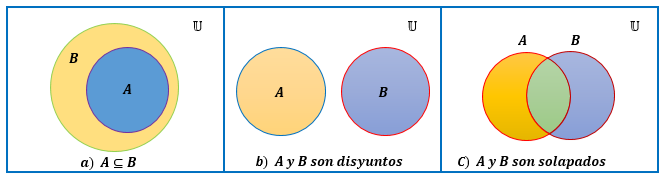
Figura 2.1: Diagramas de Venn

2.1.9 Partición

Definición 2.13 (Partición) Sea \(S\) un conjunto no vacío. Una partición de \(S\) es una colección \(\left\{A_i \right\}\) de subconjuntos no vacíos de \(S\) tales que:

1. Cada \(a\) en \(S\) pertenece a uno de los subconjuntos \(A_i\).
2. Los conjuntos de \(\left\{A_i \right\}\) son mutuamente excluyentes; es decir, si \[A_i≠A_j, \textit{entonces } A_i \cap A_j= \emptyset.\]

Los subconjuntos de una partición se denominan células.

La figura 2.2 muestra la partición de un conjunto rectangular \(S\) de puntos, en cinco células, \(A_1\), \(A_2\), \(A_3\), \(A_4\), \(A_5\).

knitr::include_graphics(path = "figuras/particion.png")

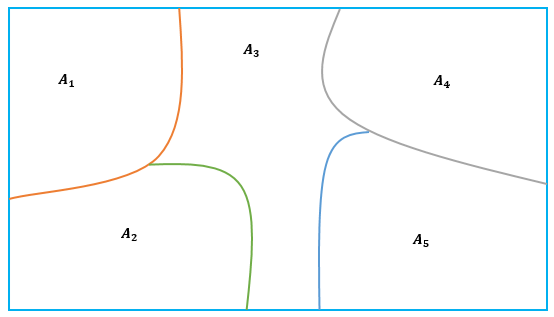
Figura 2.2: Diagrama de Venn de la partición de un conjunto rectangular \(S\)

2.2 Operaciones Con Conjuntos

En esta sección se definen las operaciones básicas entre conjuntos, tales como: intersección, unión, complemento, diferencia y diferencia simétrica. Destacando las propiedades de estas operaciones.

2.2.1 Intersección

Definición 2.14 (Intersección) La intersección de dos conjuntos \(A\) y \(B\), representada por \(A \cap B\), es el conjunto de todos los elementos que pertenecen tanto al conjunto \(A\) como al conjunto \(B\), es decir, \[A \cap B=\left\{x:x \in A \:y\: x \in B \right\}\].

La figura 2.3 muestra diagramas de Venn que ilustran la intersección de los conjunto \(A\) y \(B\).

knitr::include_graphics(path = "figuras/interseccion.png")

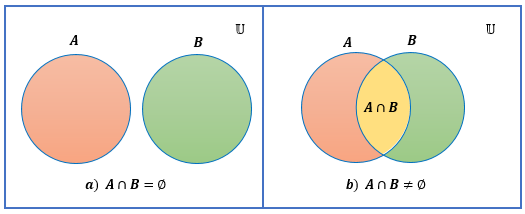
Figura 2.3: Diagrama de Venn para la intersección

2.2.1.1 Propiedades de la Intersección

1. \(A \cap \emptyset=∅\).

2. \(A \cap \mathbb{U}=A\).

3. \(A \cap A=A\). (Idempotencia)

4. \(A \cap B=B \cap A\). (Conmutativa)

5. \(A \cap B \cap C=(A \cap B) \cap C=A \cap (B \cap C)=\left(A \cap C \right) \cap B\). (Asociativa)

6. \((A \cap B) \subseteq A\).

7. \((A \cap B)\subseteq B\).

Ejemplo 2.1 (Intersección) Sea \(A=\left\{ a, b, c, d, e, f , g, h \right\}\) y \(B=\left\{ f, g, h, i, j, k, l \right\}\). Determine \(A \cap B\).

De acuerdo con la definición 2.14, la intersección de los conjuntos \(A\) y \(B\) es \[A \cap B = \left\{ f , g, h \right\}.\]

El resultado anterior, se puede obtener con el siguiente script, usando la función intersect de la distribución base de R.

A <- letters[1:8]
B <- letters[6:12]
(AyB <- intersect(A, B))

#> [1] "f" "g" "h"

El diagrama de Venn para este ejemplo se muestra con la función ggplot del paquete ggplot2. El resultado de la ejecución de esta función es la figura 2.4.

# Lista de vectores
x <- list(A, B)
# Diagrama de Venn con borde personalizado
venn <- Venn(x)
data <- process_data(venn, shape_id = "201")
ggplot() +
  # change mapping of color filling
  geom_polygon(aes(X, Y, fill = id, group = id),
    data = venn_regionedge(data),
    alpha = 0.5,
    show.legend = FALSE
  ) +
  # adjust edge size and color
  geom_path(aes(X, Y, color = id, group = id),
    data = venn_setedge(data),
    linewidth = 0.5,
    show.legend = FALSE
  ) +
  # show set label in bold
  geom_text(
    mapping = aes(X, Y, label = c("A", "B")),
    fontface = "bold.italic",
    data = venn_setlabel(data)
  ) +
  # add a alternative region name
  geom_label(
    aes(X, Y, label = count, colour = id, fill = id),
    data = venn_regionlabel(data),
    fontface = "bold",
    colour = "black",
    size = 4,
    alpha = 0.5
  ) +
  coord_equal() +
  # annotate(
  #   "text",
  #   x = 25, y = 800,
  #   label = latex2exp::TeX(
  #     "$\\mathbb{U}$",
  #     bold = TRUE,
  #     italic = TRUE
  #   )
  # ) +
  theme_void() +
  theme(
    plot.background = element_rect(
      fill = "white", size = 1,
      linetype = "blank", color = "blue"
    ),
    plot.margin = margin(
      t = 1, r = 1.2, b = 1, l = 1.2,
      unit = "cm"
    ),
    legend.title = element_blank(),
    # legend.text = element_text(
    # colour="blue", size = 8, face = "bold"
    # ),
    legend.position = "right",
    legend.spacing = unit(1, "cm"),
  ) +
  scale_colour_manual(
    values = c(
      "1" = "#E41A1C", "2" = "#377EB8", "1/2" = "#984EA3"
    ),
    aesthetics = c("colour", "fill"),
    label = c(
      TeX("$A \\setminus B$", bold = TRUE, italic = TRUE),
      TeX("$A \\cap B$", bold = TRUE, italic = TRUE),
      TeX("$B \\setminus A$", bold = TRUE, italic = TRUE)
    ),
    breaks = c("1", "2", "1/2"),
    guide = guide_legend(
      direction = "horizontal",
      title.position = "right",
      label.position = "right",
      label.hjust = 0,
      label.vjust = 0.5,
      nrow = 3,
      ncol = 1,
      byrow = TRUE,
      face = "bold",
      label.theme = element_text(
        angle = 0,
        size = 10,
      )
    )
  )

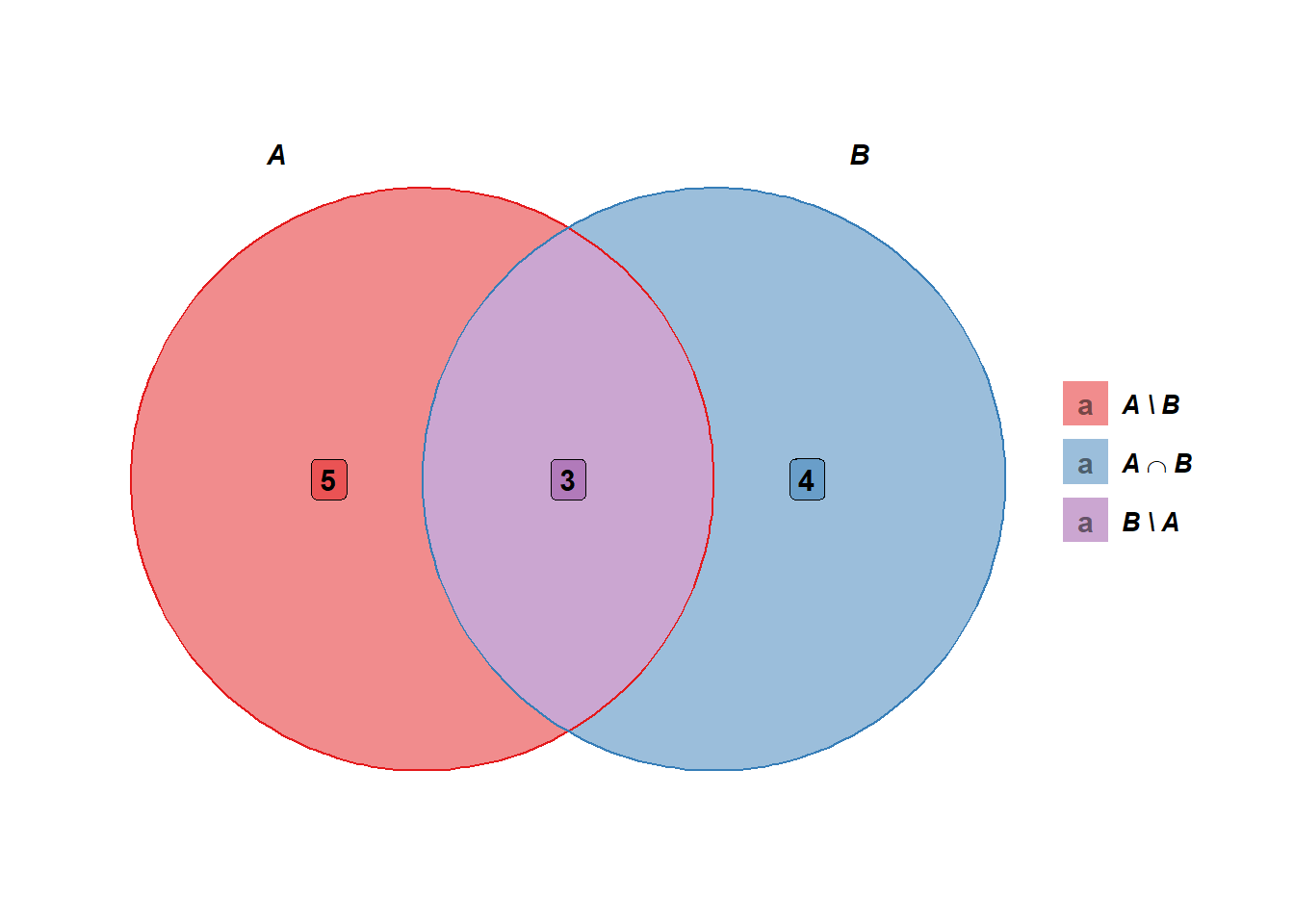
Figura 2.4: Diagrama de Venn para el ejemplo 2.1

Ejemplo 2.2 (Intersección) Dados los conjuntos \(A=\left\{ 1, 2, 3, 4, 5 \right\}\), \(B=\left\{ 2, 3, 4, 5, 6, 7 \right\}\) y \(C=\left\{ 5, 6, 7, 8, 9, 10 \right\}\). Determine \(A \cap B \cap C\).

Extendiendo la definición 2.14 para tres conjuntos, la intersección de los conjuntos \(A\), \(B\) y \(C\) son los elementos que se repiten en los tres conjuntos, es decir: \[A \cap B \cap C = \left\{5 \right\}.\]

El resultado anterior, se puede obtener con el siguiente script, usando la función intersect de la distribución base de R.

A <- 1:5
B <- 2:7
C <- 5:10
(AyByC <- intersect(intersect(A, B), C))

#> [1] 5

El Diagrama de Venn para este ejemplo se muestra en la figura 2.5.

# Lista de vectores
x <- list(A, B, C)
# Diagrama de Venn con borde personalizado
venn <- Venn(x)
data <- process_data(venn)
ggplot() +
  # change mapping of color filling
  geom_polygon(aes(X, Y, fill = id, group = id),
    data = venn_regionedge(data),
    alpha = 0.5,
    show.legend = FALSE
  ) +
  # adjust edge size and color
  geom_path(aes(X, Y, color = id, group = id),
    data = venn_setedge(data),
    linewidth = 0.5,
    show.legend = FALSE
  ) +
  # show set label in bold
  geom_text(aes(X, Y, label = c("A", "B", "C")),
    fontface = "bold.italic",
    data = venn_setlabel(data)
  ) +
  # add a alternative region name
  geom_label(
    mapping = aes(
      X, Y, label = count, colour = id, fill = id
    ),
    data = venn_regionlabel(data),
    fontface = "bold",
    color = "black",
    size = 4,
    alpha = 0.5
  ) +
  coord_equal() +
  # annotate(
  #   "text",
  #   x = -2, y = -13,
  #   label = latex2exp::TeX(
  #     "$\\mathbb{U}$",
  #     bold = TRUE,
  #     italic = TRUE
  #   )
  # ) +
  theme_void() +
  theme(
    plot.background = element_rect(
      fill = "white", size = 1,
      linetype = "blank"
    ),
    plot.margin = margin(
      t = 1, r = 1.2, b = 1, l = 1.2,
      unit = "cm"
    ),
    legend.title = element_blank(),
    # legend.text = element_text(
    #   colour="blue", size = 8, face = "bold"
    # ),
    legend.position = "right",
    legend.spacing = unit(1, "cm"),
  ) +
  scale_colour_manual(
    values = c(
      "1" = "#E41A1C", "2" = "#377EB8",
      "3" = "#4DAF4A", "1/2" = "#984EA3",
      "1/3" = "#FF7F00", "2/3" = "#FFFF33",
      "1/2/3" = "#A65628"
    ),
    aesthetics = c("colour", "fill"),
    label = c(
      TeX(
        "$A \\setminus \\left(B \\cup C \\right)$", 
        bold = TRUE, italic = TRUE
      ),
      TeX(
        "$B \\setminus \\left(A \\cup C \\right)$", 
        bold = TRUE, italic = TRUE
      ),
      TeX(
        "$C \\setminus \\left(A \\cup B \\right)$", 
        bold = TRUE, italic = TRUE
      ),
      TeX(
        "$\\left(A \\cap B \\right) \\setminus \\left(A \\cap B \\cap C \\right)$", 
        bold = TRUE, italic = TRUE
      ),
      TeX(
        "$\\left(A \\cap C \\right) \\setminus \\left(A \\cap B \\cap C \\right)$", 
        bold = TRUE, italic = TRUE
      ),
      TeX(
        "$\\left(B \\cap C \\right) \\setminus \\left(A \\cap B \\cap C \\right)$", 
        bold = TRUE, italic = TRUE
      ),
      TeX(
        "$A \\cap B \\cap C$", 
        bold = TRUE, italic = TRUE
      )
    ),
    breaks = c(
      "1", "2", "3", "1/2", "1/3", "2/3", "1/2/3"
    ),
    guide = guide_legend(
      direction = "horizontal",
      title.position = "right",
      label.position = "right",
      label.hjust = 0,
      label.vjust = 0.5,
      nrow = 7,
      ncol = 1,
      byrow = TRUE,
      face = "bold",
      label.theme = element_text(
        angle = 0,
        size = 10,
      )
    )
  )

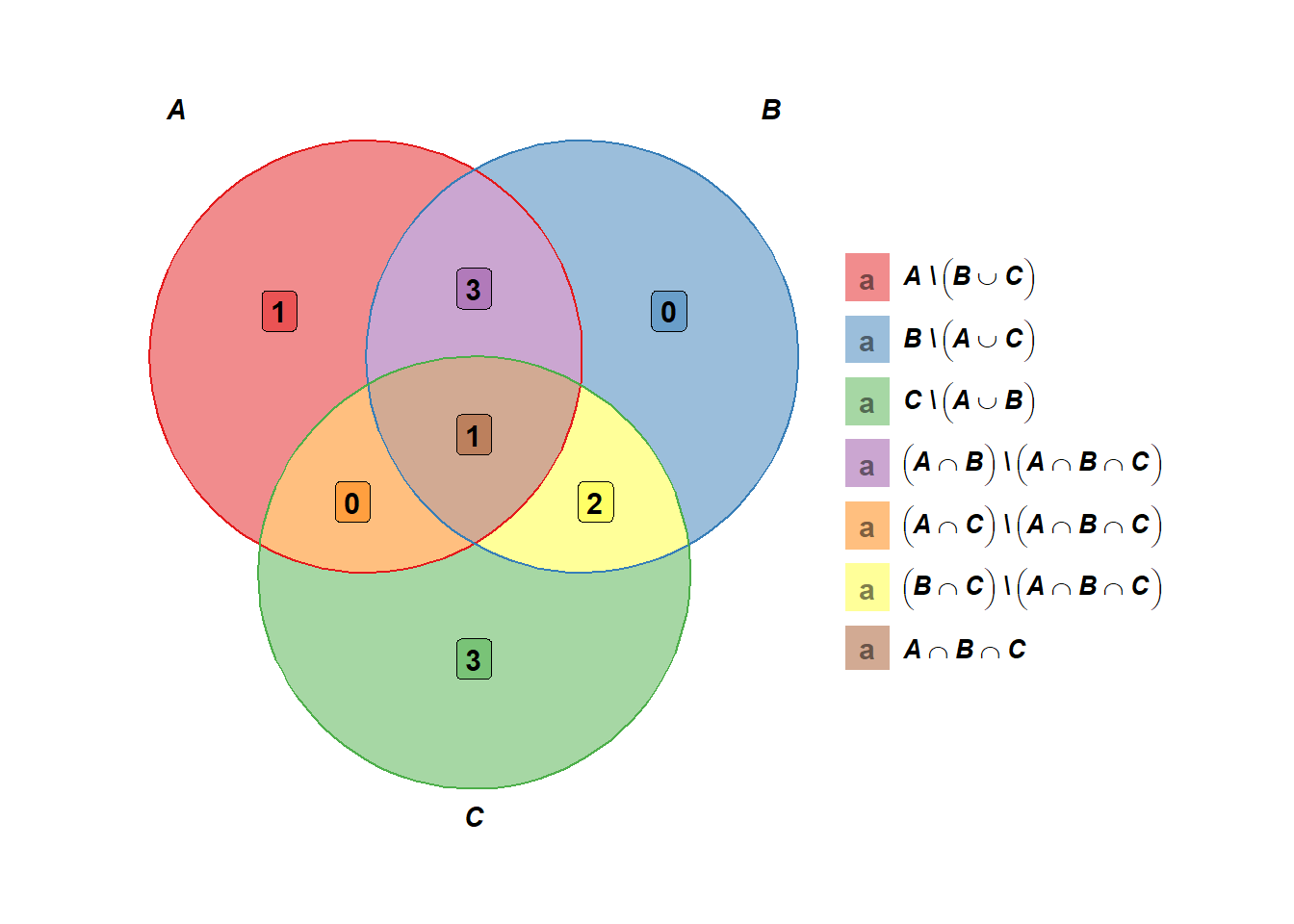
Figura 2.5: Diagrama de Venn para el ejemplo 2.2

2.2.2 Unión

Definición 2.15 (Unión) La unión de dos conjuntos \(A\) y \(B\), representada por \(A \cup B\), es el conjunto de todos los elementos que pertenecen al conjunto \(A\) o al conjunto \(B\) o a ambos, es decir, \[A∪B=\left\{x:x \in A \textit{ o } x \in B\right\}.\]

La figura 2.6 muestra diagramas de Venn que ilustran la unión de los conjunto \(A\) y \(B\).

knitr::include_graphics(
  path = "figuras/union.png"
)

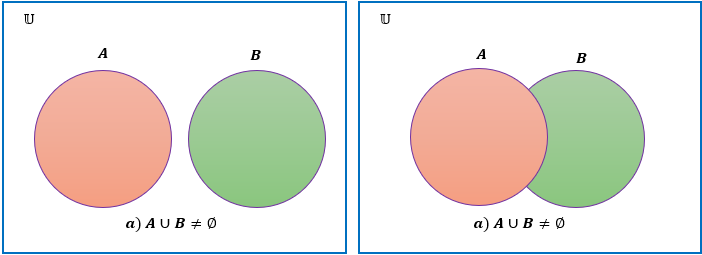
Figura 2.6: Diagrama de Venn para la Unión

2.2.2.1 Propiedades de la Unión

1. \(A \cup ∅=A\).

2. \(A \cup \mathbb{U}=\mathbb{U}\).

3. \(A \cup A=A\). (Idempotencia)

4. \(A \cup B=B \cup A\). (Conmutativa)

5. \(A \cup B \cup C=(A \cup B) \cup C=A \cup (B \cup C)=\left(A \cup C \right) \cup B\). (Asociativa)

6. \(A \subseteq (A \cup B)\).

7. \(B\subseteq(A \cup B)\).

8. \(A \cap (B \cup C)=(A \cap B) \cup (A \cap C)\). (Distributiva de la intersección)

9. \(A \cup (B \cap C)=(A \cup B) \cap (A \cup C)\). (Distributiva de la unión)

Ejemplo 2.3 (Unión) Dados los conjuntos \(A\), \(B\), especificados en el ejemplo 2.1, determine \(A \cup B\).

De acuerdo con la definición 2.15, la unión de los conjuntos \(A\) y \(B\) es \[A \cup B = \left\{a , b, c, d, e, f, g, h, i, j, k, l \right\}.\]

El resultado anterior, se puede obtener con el siguiente script, usando la función union de la distribución base de R.

A <- letters[1:8]
B <- letters[6:12]
(AoB <- union(A, B))

#>  [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l"

Ejemplo 2.4 (Unión) Dados los conjuntos \(A\), \(B\), \(C\), especificados en el ejemplo 2.2, determine \(A \cup B \cup C\).

De acuerdo con la definición 2.15, la unión de los conjuntos \(A\) y \(B\) es \[A \cup B \cup C= \left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \right\}.\]

El resultado anterior, se puede obtener con el siguiente script, usando la función union de la distribución base de R.

A <- 1:5
B <- 2:7
C <- 5:10
(AoBoC <- union(union(A, B), C))

#>  [1]  1  2  3  4  5  6  7  8  9 10

2.2.3 Complemento

Definición 2.16 (Complemeto) El complemento absoluto o, simplemente, el complemento de un conjunto \(A\), representado por \(A^c\), es el conjunto de elementos que pertenecen a \(\mathbb{U}\) pero que no pertenecen a \(A\), es decir, \[A^c=\left\{x:x∈\mathbb{U},x \notin A\right\}.\]

Algunos textos representan el complemento de \(A\) mediante \(A'\) o \(\bar{A}\).

La figura 2.7 muestra el diagramas de Venn para \(A^c\). La zona coloreada en verde representa el conjunto \(A^c\).

knitr::include_graphics(path = "figuras/complemento.png")

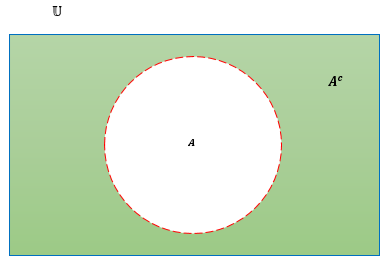
Figura 2.7: Diagrama de Venn para el complemento

2.2.3.1 Propiedades del Complemento

1. \(\left(A^c \right)^c=A\). (Propiedad Involutiva)

2. \(A \cup A^c = \mathbb{U}\)

3. \(A \cap A^c=\emptyset\)

4. \(\mathbb{U}^c=\emptyset\)

5. \(\emptyset^c=\mathbb{U}\)

2.2.3.2 Leyes de Morgan

1. \(\left(A \cup B \right)^c=A^c \cap B^c\)

2. \(\left(A \cap B \right)^c=A^c \cup B^c\)

Ejemplo 2.5 (Complemento) Dado el conjunto universal \(\mathbb{U}\), el cual representa el alfabeto inglés (no contiene la letra ñ). Dado el conjunto \[A= \left\{l, w, z, f, s, m, y, v, c, p, q, x, k, b, j \right\}.\] Determine el complemento de A \(\left(A^c \right)\).

De acuerdo con la definición 2.16, el complemento de \(A\) es: \[ A^c = \left\{a, d, e, g, h, i, n, o, r, t, u \right\}. \]

El resultado anterior, se puede obtener con el siguiente script, usando la función setdiff de la distribución base de R.

A <- c(
  "l", "w", "z", "f", "s", "m", "y", "v",
  "c", "p", "q", "x", "k", "b", "j"
)
U <- letters
(Ac <- setdiff(U, A))

#>  [1] "a" "d" "e" "g" "h" "i" "n" "o" "r" "t" "u"

Con el siguiente trozo de código se verifican las propiedades del complemento, dadas en la sección 2.2.3.1, para el ejemplo en cuestión.

Acc <- setdiff(U, Ac)
CV <- as.character(c())
(a <- setequal(Acc, A))
(b <- setequal(union(A, Ac), U))
(c <- setequal(intersect(A, Ac), CV))
(d <- setequal(setdiff(U, U), CV))

2.2.4 Diferencia

Definición 2.17 (Diferencia) El complemento relativo de un conjunto \(B\) con respecto a un conjunto \(A\), o, simplemente, la diferencia entre \(A\) y \(B\), representado por \(A \setminus B\), es el conjunto de elementos que pertenecen a \(A\) pero que no pertenecen a \(B\), es decir, \[A \setminus B=\left\{x:x \in A,x \notin B \right\}.\] El conjunto \(A \setminus B\) se lee “\(A\) menos \(B\)”. Algunos textos representan \(A \setminus B\) mediante \(A-B\) o \(A \sim B\).

La figura 2.8 muestra el diagramas de Venn para \(A \setminus B\) y \(B \setminus A\).

knitr::include_graphics(
  path = "figuras/diferencia.png"
)

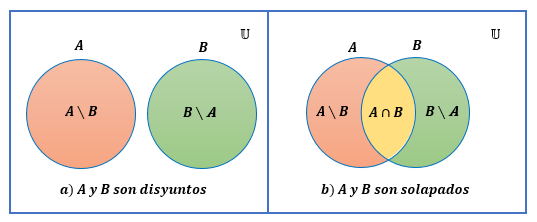
Figura 2.8: Diagrama de Venn para la diferencia

Si se tienen los conjuntos \(A\), \(B\) y \(C\); el conjuntos \(A \cup B \cap C\) queda particionado en siete conjuntos, seis de los cuales están determinados por la operación diferencia. Tal como se muestra en la figura 2.9.

knitr::include_graphics(
  path = "figuras/diferencia_3.png"
)

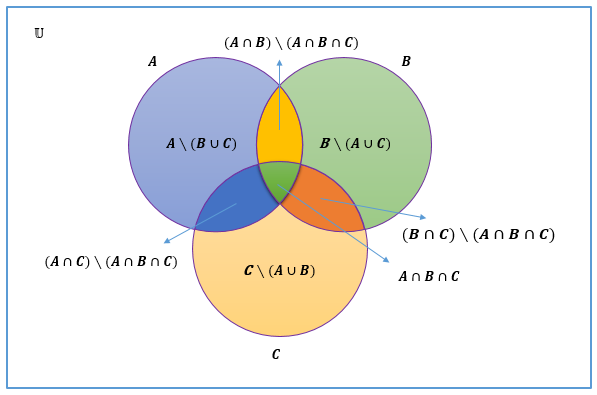
Figura 2.9: Diagrama de Venn para la diferencia dados los conjuntos \(A\), \(B\) y \(C\)

2.2.4.1 Propiedades de la Diferencia

1. \(A \setminus B \neq B \setminus A\) (la diferencia no es conmutativa).

2. \(A \setminus B = A \cap B^c \:o\: B \setminus A = B \cap A^c\).

3. \(\mathbb{U} \setminus A=A^c\)

4. \((A \setminus B) \cap (B \setminus A )=\emptyset\)

5. \(A \setminus B \subseteq A\)

Ejemplo 2.6 (Diferencia) Se tiene el conjunto universal \(\mathbb{U}\) representado por el alfabeto inglés. Por otro lado, se tienen los conjunto \(A= \left\{d, s, l, y, h, t, b, u, f, n \right\}\) y \(B= \left\{p, y, u, m, k, f, r, j, h, n \right\}\). Determine \(A \setminus B\) y \(B \setminus A\).

De acuerdo con la definición 2.17, \(A\) menos \(B\) es: \[A \setminus B = \left\{d, s, l, t, b \right\}.\]

Mientras que \(B\) menos \(A\) es: \[B \setminus A = \left\{p, m, k, r, j \right\}.\]

El resultado anterior se puede obtener con el siguiente script, usando la función setdiff de la distribución base de R.

U <- letters
A <- c(
  "d", "s", "l", "y", "h", "t", "b", "u",
  "f", "n"
)
B <- c(
  "p", "y", "u", "m", "k", "f", "r", "j",
  "h", "n"
)
(AmenosB <- setdiff(A, B))
(BmenosA <- setdiff(B, A))

#> [1] "d" "s" "l" "t" "b"
#> [1] "p" "m" "k" "r" "j"

Las propiedades de la diferencia descritas en la sección 2.2.1.1 se pueden verificar en este ejercicio por medio del siguiente script.

(a <- setequal(AmenosB, BmenosA))
(b <- setequal(AmenosB, intersect(A, setdiff(U, B))))
(c <- setequal(setdiff(U, A), setdiff(U, A)))
(d <- setequal(intersect(AmenosB, BmenosA), CV))

#> [1] FALSE
#> [1] TRUE
#> [1] TRUE
#> [1] TRUE

2.2.5 Diferencia Simétrica

Definición 2.18 (Diferencia simétrica) La diferencia simétrica de los conjuntos \(A\) y \(B\), representado por \(A \oplus B\), es el conjunto de elementos que pertenecen \(A\) o a \(B\), pero no a ambos. Es decir, \(A \oplus B=(A \cup B) \setminus (A \cap B)\) o \(A \oplus B=(A \setminus B) \cup (B \setminus A)\). Algunos textos representan \(A \oplus B\) mediante \(A \triangleright B\).

La figura 2.10 muestra el diagramas de Venn para \(A \oplus B\). El Área coloreada representa el conjunto \(A \oplus B\).

knitr::include_graphics(
  path = "figuras/diferenciasimetrica.png"
)

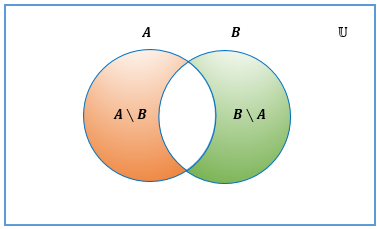
Figura 2.10: Diagrama de Venn para \(A \oplus B\)

La diferencia simétrica de los conjuntos \(A\), \(B\) y \(C\), es decir, \(A \oplus B \oplus C\) se puede apreciar en el siguiente diagrama de Venn (figura 2.11).

knitr::include_graphics(
  path = "figuras/diferenciasimetrica_3.png"
)

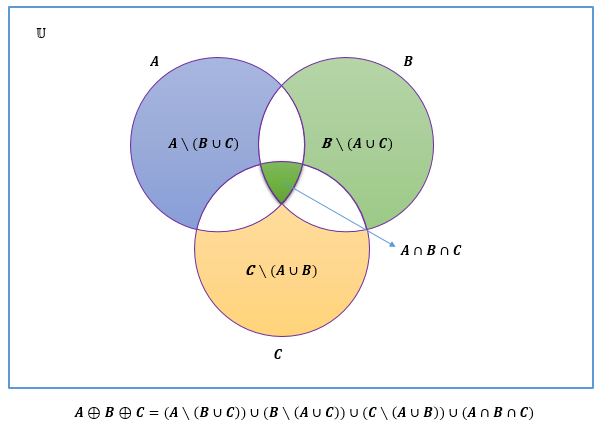
Figura 2.11: Diagrama de Venn para \(A \oplus B \oplus C\)

2.2.5.1 Propiedades de la Diferencia Simétrica

1. \(A \oplus B=B \oplus A\) (conmutativa)

2. \(A \oplus B \oplus C=(A \oplus B) \oplus C=A \oplus (B \oplus C)=(A \oplus C) \oplus B\) (asociativa)

Ejemplo 2.7 (Diferencia Simétrica) Dados los conjuntos \(A\), \(B\), especificados en el ejemplo 2.6, determine \(A \oplus B\) y \(B \oplus A\) y verifique la propiedad conmutativa de la diferencia simétrica.

De acuerdo con la definición 2.18 \[A \oplus B= \left\{d, s, l, t, b, p, m, k, r, j \right\}\], mientras que \[B \oplus A= \left\{p, m, k, r, j, d, s, l, t, b \right\}.\]

Note que \(A \oplus B = B \oplus A\), dado que ambos conjuntos contienen los mismos elementos. (Revise la definición 2.8).

El resultado anterior, se puede obtener con el siguiente script.

A <- c("d", "s", "l", "y", "h", "t", "b", "u", "f", "n")
B <- c("p", "y", "u", "m", "k", "f", "r", "j", "h", "n")
AmenosB <- setdiff(A, B)
BmenosA <- setdiff(B, A)
(AomasB <- setdiff(union(A, B), intersect(A, B)))
(BomasA <- setdiff(union(B, A), intersect(B, A)))
setequal(AomasB, BomasA)
# Otra forma de obtener la diferencia simétrica
(AomasB_2 <- union(AmenosB, BmenosA))
(BomasA_2 <- union(BmenosA, AmenosB))
setequal(AomasB_2, BomasA_2)

#>  [1] "d" "s" "l" "t" "b" "p" "m" "k" "r" "j"
#>  [1] "p" "m" "k" "r" "j" "d" "s" "l" "t" "b"
#> [1] TRUE
#>  [1] "d" "s" "l" "t" "b" "p" "m" "k" "r" "j"
#>  [1] "p" "m" "k" "r" "j" "d" "s" "l" "t" "b"
#> [1] TRUE

2.2.6 Principios para Determinar el Tamaño de un Conjunto

1. Sean \(A\) y \(B\) conjuntos finitos disyuntos. Entonces \(A \cup B\) es finito y \[ \begin{equation} n \left(A \cup B \right) = n\left(A \right) + n\left(B \right). \tag{2.1} \end{equation} \]

2. Sean \(A\) y \(B\) conjuntos finitos. Entonces \[ \begin{equation} n \left(A \setminus B \right)=n(A) - n(A \cap B). \tag{2.2} \end{equation} \]

3. Suponiendo que \(A\) es un subconjunto del conjunto Universal \(\mathbb{U}\). Entonces \[ \begin{equation} n \left(A^c \right)=n \left(\mathbb{U} \right)-n \left(A \right). \tag{2.3} \end{equation} \]

4. Principio de Inclusión-Exclusión Sean \(A\) y \(B\) conjuntos finitos. Entonces \(A∩B\) y \(A∪B\) son finitos y \[ \begin{equation} n \left( A \cup B \right)=n \left(A \right) + n \left(B \right) - n \left(A \cap B \right). \tag{2.4} \end{equation} \] Es decir, el número de elementos que están en \(A\) o en \(B\) (o ambos) se encuentran sumando primero \(n \left(A \right)\) y \(n \left(B \right)\) (inclusión) y luego restando \(n \left(A \cap B \right)\) (exclusión), puesto que sus elementos fueron contados dos veces. Fíjese que si los conjuntos \(A\) y \(B\) son disyuntos, entonces \[ n \left(A \cup B \right)=n\left(A \right)+n \left(B \right), \] dado que \(A \cap B = \emptyset\). Este resultado se puede extender para tres conjuntos de la siguiente manera: Supongamos que \(A\), \(B\), \(C\) son tres conjuntos finitos. Entonces \(A \cup B \cup C\) es finito y \[ \begin{align*} n \left(A \cup B \cup C \right) = \:\: & n \left(A \right) + n \left(B \right) + n \left(C \right) - n \left(A \cap B \right) - n \left(A \cap C \right)\\ &- n \left(B \cap C \right) + n \left(A \cap B \cap C \right). \tag{2.5} \end{align*} \]

5. Sean \(A\) y \(B\) conjuntos finitos. Entonces \(A \oplus B\) es finito y \[ \begin{equation} n \left(A \oplus B \right)=n \left(A \right) + n \left(B \right) - 2n \left(A \cap B \right). \tag{2.6} \end{equation} \] Se excluyen dos veces el número de elementos en \(A \cap B\) ya que estos están contenidos en \(A\) y en \(B\).

El principio anterior se puede extender a tres conjuntos de la siguiente manera: Supongamos que \(A\), \(B\), \(C\) son tres conjuntos finitos. Entonces \(A∪B∪C\) es finito y \[ \begin{align*} n \left( A \oplus B \oplus C \right) =\:\: & n \left(A \right)+n\left(B \right)+n \left(C \right)-2n \left(A \cap B \right)-2n \left(A \cap C \right)\\ &-2n \left(B \cap C \right)+4n \left(A \cap B \cap C \right). \tag{2.6} \end{align*} \]

6. Supongamos que \(A\), \(B\), \(C\) son tres conjuntos finitos. Entonces el número de elementos que están en dos de los tres conjuntos queda determinado por \[ \begin{align*} n \left[ \left(A \cup B \cup C \right) \setminus A \oplus B \oplus C \right] = \:\: & n \left(A \cap B \right) + n \left(A \cap C \right) + n \left(B \cap C \right)\\ &- 3n \left(A \cap B \cap C \right). \tag{2.7} \end{align*} \]

7. Supongamos que \(A\), \(B\), \(C\) son tres conjuntos finitos. Entonces el número de elementos que están exactamente en uno de los tres conjuntos queda determinado por \[ \begin{align*} n \left[ \left(A \oplus B \oplus C \right) \setminus \left(A \cap B \cap C \right) \right] = \:\: & n\left(A \right)+n \left(B \right)+n \left(C \right)-2n \left(A \cap B \right)-2n \left(A \cap C \right)\\ &-2n \left(B \cap C \right)+3n \left(A \cap B \cap C \right). \tag{2.8} \end{align*} \]

Ejemplo 2.8 (Tamaño de un Conjunto) Los estudiantes del segundo semestre de la Licenciatura en Estadísticas de la UDONE deben cursar las asignaturas Matemáticas II y Probabilidad. Se les aplicó una encuesta a 50 de estos estudiantes al final del semestre para ver si habían aprobados estas asignaturas. Las respuestas se resumen a continuación: 25 estudiantes aprobaron Matemáticas II, 20 estudiantes aprobaron Probabilidades y cinco estudiantes aprobaron ambas asignaturas. Encuentre el número de estudiantes que: a) aprobaron Probabilidad solamente, b) no aprobaron Probabilidad, c) aprobaron Matemáticas II o Probabilidad (o ambas), d) no aprobaron ninguna de las dos asignaturas y e) aprobaron una de las asignaturas.

Sea \(\mathbb{U}\) el conjunto universal formado por los 50 alumnos encuestados, \(M\) el conjunto de los alumnos que aprobaron Matemáticas II y \(P\) los alumnos que aprobaron probabilidades. Entonces, los datos anteriores se pueden expresar de la siguiente manera: \(\mathbb{U} = 50\), \(M = 25\), \(P = 20\) y \(M \cap P = 5\).

1. El número de estudiantes que aprobaron probabilidad solamente es:

\[ \begin{align*} n \left(P \setminus M \right) & = n\left(P \right) - n\left ( P \cap M \right )\\ & = 20 - 5 \\ & = 15. \end{align*} \]

2. El número de estudiantes que no aprobaron Probabilidad es:

\[ \begin{align*} n \left( P^c \right) & = n\left (\mathbb{U} \right ) - n\left( P \right )\\ & = 50 - 20 \\ & = 30. \end{align*} \]

3. El número de estudiantes que aprobaron Matemáticas II o Probabilidad (o ambas) es:

\[ \begin{align*} n \left(M \cup P \right) & = n\left (M \right ) + n\left( P \right ) - n\left (M \cap P \right )\\ & =25 + 20 - 5 \\ & = 40. \end{align*} \]

4. El número de estudiantes que no aprobaron ninguna de las dos asignaturas es:

\[ \begin{align*} n \left(M^c \cap P^c \right) & = n\left ( \left (M \cup P \right )^c \right )= n\left( \mathbb{U} \right ) - n\left (M \cup P \right )\\ & =50 - 40 \\ & = 10. \end{align*} \]

4. El número de estudiantes que aprobaron una de las asignaturas es:

\[ \begin{align*} n \left(M \oplus P \right) & = n\left (M \right ) + n\left( P \right ) - 2n\left (M \cap P \right )\\ & =25 + 20 - 2(5) \\ & = 35. \end{align*} \]

Los resultados anteriores se resumen en el diagrama de Venn que se muestra en la figura 2.12. Este diagrama se ha generado con la función ggplot del paquete ggplot2.

# Diagrama de Venn con borde personalizado
venn <- ggVennDiagram::Venn(
  list(M = 1:25, P = 21:40)
)
data <- ggVennDiagram::process_data(venn, shape_id = "201")
ggplot() +
  # change mapping of color filling
  geom_polygon(aes(X, Y, fill = id, group = id),
    data = venn_regionedge(data),
    alpha = 0.5,
    show.legend = FALSE
  ) +
  # adjust edge size and color
  geom_path(aes(X, Y, color = id, group = id),
    data = venn_setedge(data),
    linewidth = 0.5,
    show.legend = FALSE
  ) +
  # show set label in bold
  geom_text(
    mapping = aes(
      X, Y, label = c("Probabilidad", "Matemáticas II")
    ),
    fontface = "bold.italic",
    data = venn_setlabel(data)
  ) +
  # add a alternative region name
  geom_label(
    aes(X, Y, label = count, colour = id, fill = id),
    data = venn_regionlabel(data),
    fontface = "bold",
    colour = "black",
    size = 4,
    alpha = 0.5
  ) +
  # annotate(
  #   "text",
  #   x = 25, y = 800,
  #   label = latex2exp::TeX(
  #     "$\\mathbb{U}$",
  #     bold = TRUE,
  #     italic = TRUE
  #   )
  # ) +
  coord_equal() +
  theme_void() +
  theme(
    plot.background = element_rect(
      fill = "white", size = 1,
      linetype = "blank", color = "blue"
    ),
    plot.margin = margin(
      t = 1, r = 2, b = 1, l = 2,
      unit = "cm"
    ),
    legend.position = "none"
  ) +
  scale_colour_manual(
    values = c(
      "1" = "#E41A1C", "2" = "#377EB8",
      "12" = "#984EA3"
    ),
    aesthetics = c("colour", "fill")
  )

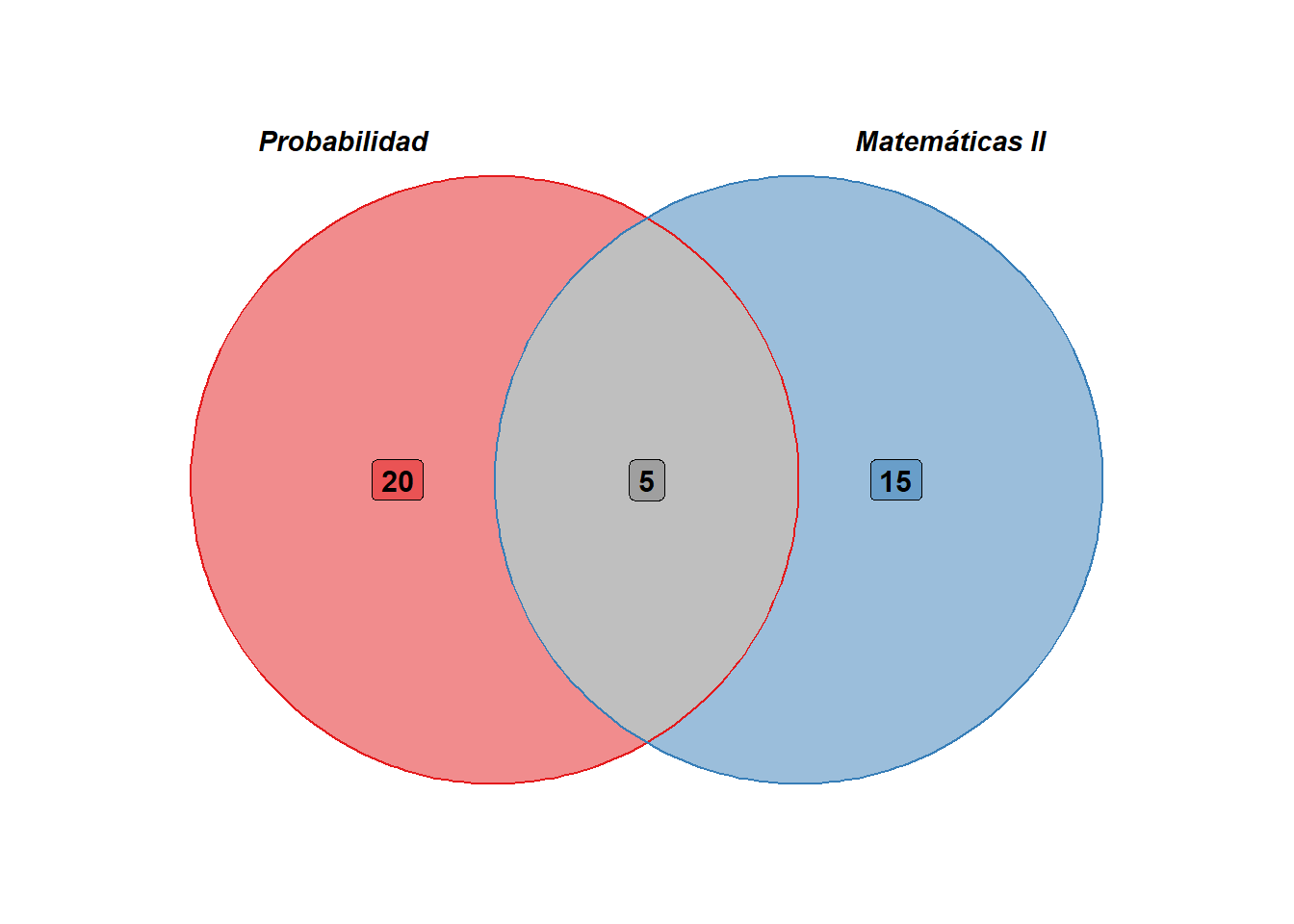
Figura 2.12: Diagrama de Venn del ejemplo 2.8

Ejemplo 2.9 (Tamaño de un Conjunto) De 140 alumnos de un centro de idiomas se sabe que: 62 estudian inglés, 52 estudian francés, 54 estudian alemán, 18 estudian inglés y francés, 20 estudian francés y alemán, 17 solo estudian alemán y 8 estudian los tres idiomas ¿Cuántos alumnos estudian otros idiomas?

Sea \(\mathbb{U}\) el conjunto universal formado por los 140 alumnos, \(I\) el conjunto de los alumnos que estudian inglés, \(F\) el conjunto de los alumnos que estudian francés y \(A\) el conjuntos de los alumnos que estudian alemán. Entonces, los datos anteriores se pueden reescribir de la siguiente manera: \(n \left(I \right) = 62\), \(n \left(F \right) = 52\), \(n \left(A \right) = 54\), \(n \left(I \cap F \right) = 18\), \(n \left(F \cap A \right) = 20\), \(n \left(A \setminus \left(I \cup F \right) \right) = 17\) y \(\left(I \cap F \cap A \right) = 8\).

Los alumnos que estudian otros idiomas son

\[ n \left( \left(I \cup F \cup A \right)^c \right)= n \left( \mathbb{U} \right) - n \left(I \cup F \cup A \right). \]

Note que para hallar \(n \left(I \cup F \cup A \right)\) es necesario hallar \(n \left(I \cap A \right)\). Pero,

\[ \begin{align*} n \left(A \setminus \left(I \cup F \right) \right) & = n \left(A \right) - n \left(A \cap \left(I \cup F \right) \right) \\ & = n \left(A \right) - n \left( \left(A \cap I \right) \cup \left(A \cap F \right) \right) \\ & = n \left(A \right)-\left[ n \left(A \cap I \right) + n \left(A \cap F \right) - n \left( \left(A \cap I \right) \cap \left(A \cap F \right) \right) \right] \\ & = n \left(A \right) - n\left(A \cap I \right)- n\left(A \cap F \right) + n\left(I \cap F \cap A \right) \\ 17& = 54 - n\left(A \cap I \right) -20 + 8. \end{align*} \]

De donde se obtiene que \(n\left(I \cap A \right)=25\). Luego,

\[ \begin{align*} n \left(I \cup F \cup A \right) = \:\: & n \left(I \right) + n \left(F \right) + n \left(A \right) - n \left(I \cap F \right) - n \left(I \cap A \right)\\ &- n \left(F \cap A \right) + n \left(I \cap F \cap A \right)\\ = \:\: & 62 + 52 + 54 - 18 -25 -20 + 8\\ = \:\: & 113. \end{align*} \]

Por último,

\[ \begin{align*} n \left( \left(I \cup F \cup A \right)^c \right) & = n \left( \mathbb{U} \right) - n \left(I \cup F \cup A \right)\\ & = 140 - 113\\ & = 27. \end{align*} \]

Los resultados anteriores se resumen en el diagrama de Venn indicado en la figura 2.13 . Este diagrama se ha generado con la función ggplot del paquete ggplot2.

venn <- ggVennDiagram::Venn(
  list(
    I = letters[1:10], F = letters[3:12], A = letters[6:15]
  )
)
data <- ggVennDiagram::process_data(venn)
ggplot() +
  # change mapping of color filling
  geom_polygon(aes(X, Y, fill = id, group = id),
    data = venn_regionedge(data),
    alpha = 0.5,
    show.legend = FALSE
  ) +
  # adjust edge size and color
  geom_path(aes(X, Y, color = id, group = id),
    data = venn_setedge(data),
    linewidth = 0.5,
    show.legend = FALSE
  ) +
  # show set label in bold
  geom_text(
    aes(
      X, Y, label = c(
        "Inglés", "Francés", "Alemán"
      )
    ),
    fontface = "bold.italic",
    size = 4,
    data = venn_setlabel(data)
  ) +
  # add a alternative region name
  geom_label(
    mapping = aes(
      X, Y, label = c(27, 22, 17, 10, 17, 12, 8), 
      colour = id, fill = id
    ),
    data = venn_regionlabel(data),
    show.legend = FALSE,
    fontface = "bold",
    color = "black",
    size = 4,
    alpha = 0.5
  ) +
  # annotate(
  #   "text",
  #   x = 25, y = 800,
  #   label = latex2exp::TeX(
  #     "$\\mathbb{U}$",
  #     bold = TRUE,
  #     italic = TRUE
  #   )
  # ) +
  coord_equal() +
  theme_void() +
  xlim(-5, 9) +
  theme(
    plot.background = element_rect(
      fill = "white", size = 1,
      linetype = "blank", color = "blue"
    ),
    plot.margin = margin(
      t = 1, r = 1, b = 1, l = 1,
      unit = "cm"
    ),
    legend.title = element_blank(),
    # legend.text = element_text(
    #   colour="blue", size = 8, face = "bold"
    # ),
    legend.position = "right",
    legend.spacing = unit(1, "cm"),
  ) +
  scale_colour_manual(
    values = c(
      "1" = "#E41A1C", "2" = "#377EB8",
      "3" = "#4DAF4A", "1/2" = "#984EA3",
      "1/3" = "#FF7F00", "2/3" = "#FFFF33",
      "1/2/3" = "#A65628"
    )
  )

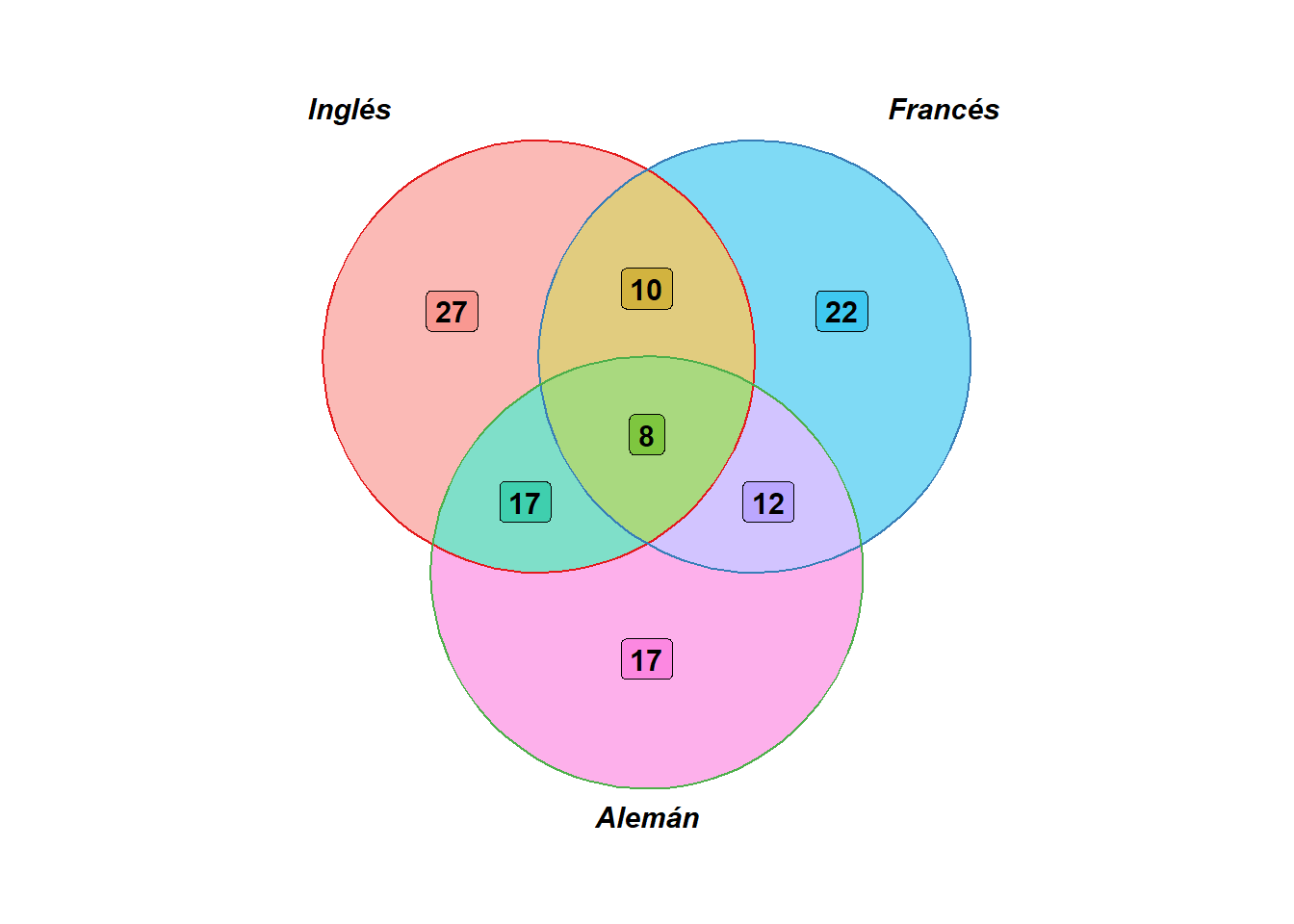
Figura 2.13: Diagrama de Venn del ejemplo 2.9

2.3 Introducción a la Probabilidad

En esta sección se introducen algunas definiciones que permiten entender el concepto de probabilidad, así como también, se define de manera axiomática la probabilidad de un evento. Por otro lado, se definen algunos enfoques para la asignación y cálculo de probabilidades de eventos. También, se define la probabilidad condicional y el teorema de Bayes para hacer cálculo de probabilidades de eventos dependientes e independientes.

2.3.1 Experimento Determinístico

Definición 2.19 (Experimento Determinístico) Es un experimento en el cual se puede predecir el resultado.

Ejemplo 2.10 (Experimento Determinístico) Supóngase que se deja caer desde una altura \(h\) un objeto y se anota el tiempo \(t\) que tarde el objeto en chocar con el suelo.

El experimento acá descrito es determinístico dado que cada vez que este se realice, bajo las mismas condiciones, el resultado siempre va ser el mismo, por lo que bastaría ejecutarlo una vez para saber lo que ocurrirá en replicas sucesivas del experimento. Incluso, puede conocerse este tiempo antes de realizar el experimento, dado que el tiempo está determinado por la altura a través de la siguiente relación matemática: \[ t = \sqrt{ \frac{2h}{g}}. \]

2.3.2 Experimento Aleatorio o Experiencia Aleatoria

Definición 2.20 (Experimento Aleatorio) Es un experimento en el cual no se puede predecir el resultado o en otras palabras el resultado está regido por el azar. Cada resultado posible del experimento aleatorio se denomina punto muestral.

Generalmente, el experimento aleatorio se denota con la letra griega épsilon \(\varepsilon\).

Ejemplo 2.11 (Experimento Aleatorio) Supóngase que se lanza un dado y se anota el número que aparece.

El experimento aquí descrito es aleatorio dado que el resultado obtenido en cada replica del experimento está determinado por el azar, es decir, no se puede predecir que cara mostrará el dado una vez que este se lance. En este caso, el experimento aleatorio es: \(\varepsilon: \mathit{``Lanzar \: el \: dado \: y \: anotar \: el\: resultado"}\).

2.3.3 Espacio Muestral

Definición 2.21 (Espacio Muestral) Es el conjunto que consta de todos los resultados posibles de un experimento aleatorio y se denotará con la letra \(S\). A cada uno de los resultados posibles de un experimento aleatorio se denomina punto muestral. Algunos textos representa el espacio muestral con la letra griega omega \(\Omega\).

Ejemplo 2.12 (Espacio Muestral) En el experimento de lanzar un dado y anotar el número que aparece, descrito en el ejemplo 2.11, el espacio muestral es \[ S=\left\{1,2,3,4,5,6 \right\}; \] y los puntos muestrales son \(1,2,3,4,5,6\).

2.3.3.1 Espacio Muestral Finito

Definición 2.22 (Espacio Muestral Finito) Un espacio muestral \(S\) es finito si el número de puntos muestrales de \(S\) \(\left(n \left(S \right) \right)\) es un número \(m\) entero positivo; es decir \[ n(S)=m, \:donde\: m \in \mathbb{ N }. \]

Ejemplo 2.13 (Espacio Muestral Finito) En el experimento de lanzar un dado del ejemplo 2.11, el espacio muestral se muestra en el ejemplo 2.12. Como se puede notar, este espacio muestral es finito, ya que este está constituido por 6 PUNTOS muestrales, es decir, \(n \left(S \right) = 6\).

2.3.3.2 Espacio Muestral Infinito Contable

Definición 2.23 (Espacio Muestral Infinito Contable) Un espacio muestral \(S\) es infinito contable (o numerable) si se puede establecer una correspondencia uno a uno (biunívoca) entre cada uno de los puntos muestrales de \(S\) y los números naturales \(\mathbb{ N }\).

Ejemplo 2.14 (Espacio Muestral Infinito Contable) Supóngase el experimento que consiste en anotar el número de veces en que se lanza una moneda hasta que salga una cara, entonces el espacio muestral definido sobre este experimento aleatorio es \[ S=\left\{c,sc,ssc,sssc,ssssc,\dotsc \right\}. \] Como se puede notar \(S\) es infinito numerable, dado que cada punto muestral se puede emparejar con un único número natural \(\mathbb{ N }\), como se muestra a continuación: \[ \begin{matrix} c & \Rightarrow & 1 \\ sc & \Rightarrow & 2 \\ ssc & \Rightarrow & 3 \\ sssc & \Rightarrow & 4 \\ ssssc & \Rightarrow & 5 \\ sssssc & \Rightarrow & 6 \\ \vdots & \vdots & \vdots \\ \end{matrix} \]

2.3.3.3 Evento o Suceso

Definición 2.24 (Evento) Es cualquier subconjunto del espacio muestral \(S\), cuyos elementos tienen características comunes. Sea \(A\) un evento, se dice que el evento \(A\) ocurrió si el resultado del experimento es un elemento de \(A\).

Ejemplo 2.15 (Evento) En el experimento aleatorio de lanzar un dado y anotar el número que sale, descrito en el ejemplo 2.11, los siguientes conjuntos son eventos: \[ A=\left\{1 \right\}; B=\left\{6 \right\}; C=\left\{1,3,5 \right\}; D=\left\{2,4,6 \right\}. \]

2.3.3.4 Evento Simple o Evento Elemental

Definición 2.25 (Evento Simple) Es el evento constituido por un solo punto muestral.

Ejemplo 2.15 (Evento) En el experimento aleatorio de lanzar un dado y anotar el número que sale, como se describe en el ejemplo 2.11, los siguientes eventos constituyen eventos elementales: \[ A=\left\{1 \right\}; B=\left\{2 \right\}; C=\left\{3 \right\}; D=\left\{4 \right\};E=\left\{5 \right\}; F=\left\{6 \right\}. \]

2.3.3.5 Evento Compuesto

Definición 2.26 (Evento Compuesto) Es el evento constituido por más de un punto muestral.

Ejemplo 2.15 (Evento Compuesto) En el experimento aleatorio de lanzar un dado y anotar el número que sale, referido en el ejemplo 2.11, los siguientes eventos constituyen eventos compuestos: \[ A=\left\{1,2 \right\}; B=\left\{1,3,5\right\};C=\left\{1,3,5,6 \right\}; D=\left\{1,2,3,4,5,6 \right\}. \]

2.3.3.6 Evento Imposible

Definición 2.27 (Evento Imposible) Es el evento que nunca ocurre, es decir, el evento que contiene a ningún resultado posible del espacio muestral. En otras palabras, el conjunto vació \((\emptyset)\).

2.3.3.7 Evento Seguro o Cierto

Definición 2.28 (Evento Seguro) Es el evento que siempre ocurre, es decir, el evento que contiene a todos los resultados posibles del espacio muestral. En otras palabras, el espacio muestral \(\left(S \right)\).

2.3.3.8 Eventos Mutuamente Excluyentes o Incompatibles

Definición 2.29 (Eventos Mutuamente Excluyentes) Dos eventos \(A\), \(B\) son mutuamente excluyentes si la ocurrencia de uno implica la no ocurrencia del otro. En otras palabras, se puede decir que dos sucesos son mutuamente excluyentes si ninguno de los puntos muestrales que conforman uno están contenido en el otro; por lo que \[ A \cap B=\emptyset. \]

2.3.3.9 Eventos Compatibles o Solapados

Definición 2.30 (Eventos Compatibles) Dos eventos \(A\), \(B\) se dice que son compatibles, o que no son mutuamente excluyentes o que son solapados, cuando la ocurrencia de uno no impide la ocurrencia del otro. En otros términos, los eventos comparte por lo menos un punto muestral; por lo que \[ A \cap B \neq \emptyset. \]

Nota:. Como se ha podido observar los eventos son conjunto por lo tanto toda la teoría de conjunto es aplicable a los eventos.

2.3.4 Probabilidad

Definición 2.31 (Probabilidad) Es una medida de la incertidumbre sobre la ocurrencia de un evento en particular en un experimento aleatorio.

2.3.4.1 Enfoque Clásico (o de Laplace o a Priori) de la Probabilidad

Definición 2.32 (Enfoque Clásico de la Probabilidad) Si un experimento aleatorio puede ocurrir de \(N\) maneras diferentes \(\left(n \left(S \right) = N \right)\) igualmente probables y mutuamente excluyentes, y un evento \(A\) puede ocurrir de \(n\) maneras diferentes \(\left(n \left(A \right) = n \right)\). Entonces la probabilidad de que ocurra el evento \(A\) viene dada por \[ \begin{equation} P\left(A \right)=\frac{n \left(A \right)}{n \left(S \right)} =\frac{n}{N}. \tag{2.9} \end{equation} \]

Ejemplo 2.16 (Enfoque Clásico de la Probabilidad) Supongamos que queremos conocer la probabilidad de que ocurra cara en el lanzamiento sencillo de una moneda. Dado que hay dos maneras igualmente probables como puede caer la moneda, a saber: cara (\(c\)) o sello (\(s\)) (suponiendo que no se pierda o caiga de canto). Por lo que el espacio muestral viene dado por \(S = \left\{s, c \right\}\). Sea \(A\) el evento “la moneda cae cara”, es decir, \(A = \left\{c \right\}\). Entonces, la probabilidad de que ocurra cara, según la ecuación (2.9), es: \[ P \left(A \right)=\frac{n\left(A \right)}{n\left(S \right)}=\frac{1}{2}=0,5. \] Para llegar a este resultado suponemos que la moneda es balanceada.

2.3.4.2 Enfoque Frecuentista (Empírico o a Posteriori) de la Probabilidad

Definición 2.33 (Enfoque Frecuentista de la Probabilidad) Si un experimento se repite \(N\) veces bajo las mismas condiciones y en \(n\) de los resultados ocurre un evento \(A\). Entonces, la probabilidad de que ocurra el evento \(A\) tiende a \(n/N\), conforme \(N\) tiende a infinito. Es decir, \[ \begin{equation} P\left(A \right) = \lim_{N \to \infty} \frac{n}{N}. \tag{2.10} \end{equation} \]

Ejemplo 2.17 (Enfoque Frecuentista de la Probabilidad) Se realiza un experimento bajo ciertas condiciones, el cual consiste en agregar un antibiótico a una cepa de bacterias. Una hora después de realizar el experimento encontramos que de 7.627 bacterias 4.036 murieron en 1 hora o antes. ¿Cuál es la probabilidad que tiene una bacteria de morir en una hora o antes?

Sea \(A\): “la bacteria muere en una hora o antes”, según la ecuación (2.10), \(n = 4.036\) y \(N = 7.627\). En consecuencia,la probabilidad de que ocurra \(A\) es: \[ P\left(A \right) =\frac{n}{N} =\frac{4.036}{7.627}=0,5292. \]

2.3.4.3 Enfoque Subjetivo (o Personal) de la Probabilidad

Definición 2.34 (Enfoque Subjetivo de la Probabilidad) Es el grado de creencia o de convicción que se tiene con respecto a la ocurrencia de un evento.

Ejemplo 2.18 (Probabilidad Subjetiva) A una persona se le pregunta sobre la probabilidad de que llueva, la persona mira hacia el cielo y al percatarse que el cielo está nublado dice “la probabilidad de que llueva es de un 80%”.

2.3.4.4 Axiomas de la Probabilidad

Sea \(S\) cualquier espacio muestral y \(A\) cualquier evento de éste. Se llamará función de probabilidad sobre el espacio muestral \(S\) a \(P\left(A \right)\) si satisface los siguientes axiomas:

1. \(P\left(A \right) \geq 0\) (toda probabilidad es no negativa).

2. \(P\left(S \right)=1\) (la probabilidad del espacio muestral es uno).

3. Si \(A_1, A_2, A_3, \dotsc\) es una sucesión de eventos mutuamente excluyente; es decir \(A_i \cap A_j = \emptyset\) para todo \(i \ne j\). Entonces \[ P(A_1 \cup A_2 \cup A_3 \cup \cdots)=P(A_1 )+P(A_2 )+P(A_3 )+ \cdots \]

De estos tres axiomas se desprenden los siguientes teoremas:

Teorema 2.3 La probabilidad de que ocurra el evento imposible es cero. Es decir, \[ \begin{equation} P(\emptyset)=0. \tag{2.11} \end{equation} \]

Demostración. \(S \cup \emptyset=S\) y \(S \cap \emptyset=\emptyset\). Por el axioma 3, \(P \left(S \cup \emptyset \right)=P \left(S \right)+P \left( \emptyset \right)\); pero por el axioma 2, \(P \left(S \right)=1\), y de esta manera \(P(\emptyset)=0\).

Teorema 2.4 Para cualquier evento \(A \subseteq S\), se cumple que \[ \begin{equation} 0 \le P \left(A \right) \le 1. \tag{2.12} \end{equation} \]

Demostración. Por el axioma 1 \(P(A) \ge 0\); de aquí que solo es necesario probar que \(P(A) \le 1\). \(A \cup A^c = S\) y \(A \cap A^c = \emptyset\). Por los axiomas 2 y 3, \(P \left(A \cup A^c \right)=P \left(A \right)+P \left(A^c \right)=P \left(S \right)=1\); Dado que \(P \left(A^c \right) \ge 0\), entonces \[ P \left(A \right) \le 1. \]

Teorema 2.5 (Regla del Complemento) Para cualquier evento \(A\), se tiene \[ \begin{equation} P\left(A^c \right)=1-P \left(A \right). \tag{2.13} \end{equation} \]

Demostración. Como \(A \cup A^c = S\) y \(A \cap A^c= \emptyset\). Por los axiomas 2 y 3, \(P \left(A \cup A^c \right)=P \left(A \right)+P \left(A^c \right)=P \left(S \right)=1\); De aquí que \[ P \left(A^c \right)=1-P \left(A \right). \]

Teorema 2.6 (Regla de la Diferencia) Para dos eventos cualesquiera \(A\) y \(B\) del espacio muestral \(S\), se cumple que \[ \begin{equation} P\left(A \setminus B \right)=P \left(A \right)-P\left(A \cap B \right). \tag{2.14} \end{equation} \]

Demostración. Como se muestra en la figura 2.14, \(A=\left(A\setminus B \right) \cup \left(A \cap B \right)\) donde \(A \setminus B\) y \(A \cap B\) son mutuamente excluyentes. En consecuencia, por el tercer axioma de la probabilidad definido en la sección 2.3.4.4, \[ P \left(A\right)=P \left(A \setminus B \right)+P\left(A \cap B \right). \] De donde se obtiene, \[ P \left(A \setminus B \right)=P \left(A\right)-P\left(A \cap B \right). \]

knitr::include_graphics(
  path = "figuras/regla_diferencia.png"
)

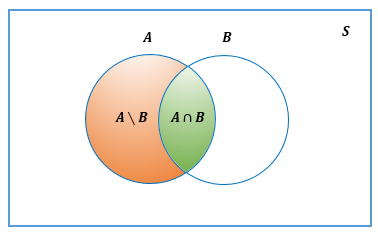
Figura 2.14: Diegrama de Venn para regla de la diferencia

Teorema 2.7 (Regla de la Adición) Para dos eventos cualesquiera \(A\) y \(B\) del espacio muestral \(S\), se cumple que \[ \begin{equation} P\left(A \cup B \right)=P \left(A \right)+P \left(B \right)-P\left(A \cap B \right). \tag{2.15} \end{equation} \]

Demostración. Como se muestra en la figura 2.15, \(A\cup B = \left(A \setminus B \right) \cup B\) donde \(A \setminus B\) y \(B\) son conjuntos mutuamente excluyentes. En consecuencia, por el tercer axioma de la probabilidad definido en la sección 2.3.4.4, \[ P \left(A \cup B\right)=P \left(A \setminus B \right)+P\left( B \right). \] De donde se obtiene, por la regla de la diferencia 2.6 \[ \begin{align*} P \left(A \cup B\right)&=P \left(A \right)- P\left(A \cap B \right)+P\left( B \right)\\ &=P \left(A \right)+P\left( B \right)- P\left(A \cap B \right). \end{align*} \]

knitr::include_graphics(
  path = "figuras/regla_adicion.png"
)

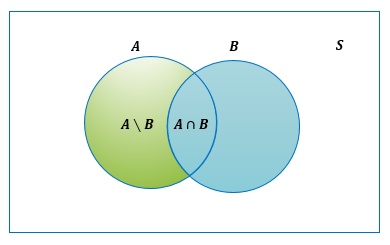
Figura 2.15: Diegrama de Venn para la regla de la adición

Teorema 2.8 (Regla de la Adición para Tres Eventos) Si \(A\), \(B\) y \(C\) son tres eventos cualesquiera del espacio muestral \(S\), entonces \[ \begin{align*} P\left(A \cup B \cup C \right)=&P \left(A \right)+P \left(B \right)+P \left(C \right)-P\left(A \cap B \right)\\ &-P\left(A \cap C \right) -P\left(B \cap C \right)+P\left(A \cup B \cup C \right). \tag{2.16} \end{align*} \]

Demostración. Al escribir \(A \cup B \cup C\) como \(A \cup \left(B \cup C \right)\), por la propiedad asociativa de la unión 2.2.2.1, y utilizando la regla de la adición 2.7 dos veces, una vez para \(P \left[A \cup \left(B \cup C \right) \right]\) y una para \(P \left( B \cup C\right)\) se obtiene \[ \begin{align*} P \left(A \cup B \cup C \right)&=P \left[A \cup \left(B \cup C \right) \right]\\ &=P \left(A \right)+P \left(B \cup C \right)-P \left[A \cap \left(B \cup C \right) \right]\\ &=P \left(A \right)+P \left(B \right)+P \left(C \right)-P \left(B \cap C \right)-P \left[A \cap \left(B \cup C \right) \right]. \end{align*} \] De la propiedad distributiva de la intersección descrita en 2.2.2.1, se sigue que \[ \begin{align*} P \left[A \cap \left(B \cup C \right) \right]&=P \left[ \left(A \cap B \right) \cup \left(A \cap C \right) \right]\\ &=P\left(A \cap B \right) + P\left(A \cap C \right)-P \left[ \left(A \cap B \right) \cap \left(B \cap C \right) \right]\\ &=P\left(A \cap B \right) + P\left(A \cap C \right)-P\left(A \cap B \cap C \right) \end{align*} \] y por tanto, se sigue que \[ \begin{align*} P \left(A \cup B \cup C \right)=&P \left(A \right)+P \left(B \right)+P \left(C \right)-P \left(B \cap C \right)\\ &-\left[P\left(A \cap B \right) + P\left(A \cap C \right)-P\left(A \cap B \cap C \right) \right]\\ =&P \left(A \right)+P \left(B \right)+P \left(C \right)-P \left(A \cap B \right)-P \left(A \cap C \right)\\ &-P \left(C \cap B \right)+P\left(A \cap B \cap C \right). \end{align*} \]

Teorema 2.8 (Regla de la Adición para \(k\) Eventos) Sean \(A_1, A_2, \dotsc, A_k\) \(k\) sucesos cualesquiera del espacio muestral \(S\). Entonces \[ \begin{align*} P\left ( \bigcup_{i=1}^{k} A_{i} \right )=&\sum_{i=1}^{k}P\left ( A_{i} \right )-\sum_{i< j=2}^{k}P\left ( A_{i} \cap A_{j} \right )+\sum_{i< j< r=3}^{k}P\left ( A_{i} \cap A_{j} \cap A_{r} \right )\\ &+\cdots +\left ( -1 \right )^{k-1}P\left ( \bigcap_{i=1}^{k} A_{i} \right). \tag{2.17} \end{align*} \]

2.3.4.5 Probabilidad Condicional

Definición 2.35 (Probabilidad Condicional) Suponga que \(B\) es un evento en un espacio muestral \(S\), tal que \(P \left(B \right) > 0\), es decir \(B \neq \emptyset\). La probabilidad de que ocurra un evento \(A\) una vez que \(B\) ha ocurrido o, en otras palabras, la la probabilidad condicional de \(A\) dado \(B\), escrita \(P \left( A \mid B \right)\), se define así: \[ \begin{equation} P \left( A \mid B \right)=\frac{P \left( A \cap B \right)}{P \left( B \right)}. \tag{2.18} \end{equation} \]

Como se ilustra en el diagrama de Venn dado en la figura 2.16, \(P \left( A \mid B \right)\) mide, en cierto sentido, la probabilidad relativa de \(A\) con respecto al espacio reducido \(B\).

knitr::include_graphics(
  path = "figuras/probabilidad_condicional.png"
)

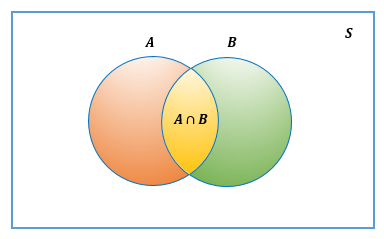
Figura 2.16: Probabilidad condicional de \(A\) dado \(B\)

Ahora, suponga que \(S\) es un espacio equiprobable. Por la definición 2.32

\[ P \left( A \cap B \right)=\frac{n\left(A \cap B \right)}{n\left(S \right)} \; y \; P \left( B \right)=\frac{n\left( B \right)}{n\left(S \right)}. \]

Luego, sustituyendo en la ecuación (2.18) se obtiene que: \[ \begin{equation} P \left( A \mid B \right)=\frac{n\left(A \cap B \right)}{n\left(B \right)}. \tag{2.19} \end{equation} \]

Ejemplo 2.19 (Probabilidad Condicional) Se lanza un par de dados equilibrados. Encuentre la probabilidad de que uno de los dados sea 2 si la suma es 6.

Dado que cada dado puede caer de 6 formas diferentes, entonces el número de formas diferentes en que pueden caer los dos dados, es decir, el número de elementos del espacio muestral \(S\), por el principio de la multiplicación 1.2, es \(6 \cdot 6=36\). En tal sentido, el espacio muestral \(S\) viene determinado por: \[ S=\begin{Bmatrix} (1,1);&(1,2);&(1,3);&(1,4);&(1,5);&(1,6);\\ (2,1);&(2,2);&(2,3);&(2,4);&(2,5);&(2,6);\\ (3,1);&(3,2);&(3,3);&(3,4);&(3,5);&(3,6);\\ (4,1);&(4,2);&(4,3);&(4,4);&(4,5);&(4,6);\\ (5,1);&(5,2);&(5,3);&(5,4);&(5,5);&(5,6);\\ (6,1);&(6,2);&(6,3);&(6,4);&(6,5);&(6,6)\\ \end{Bmatrix}. \]

Sea \(A\) el evento en el cual uno de los dados es 2, el cual viene dado por: \[ A=\begin{Bmatrix} (2,1);&(2,2);&(2,3);&(2,4);&(2,5);&(2,6);\\ (1,2);&(3,2);&(4,2);&(5,2);&(6,2)\\ \end{Bmatrix}. \] Y \(B\) el evento en el cual la suma es 6, representado por: \[ B = \begin{Bmatrix} (1,5);&(2,4);&(3,3);&(4,2);&(5,1)\\ \end{Bmatrix}. \] Entonces el evento en el cual uno de los dos dados es 2 y cuya suma es 6, es decir, \(A \cap B\), viene dado por:

\[ A \cap B=\begin{Bmatrix} (2,4);&(4,2)\\ \end{Bmatrix}. \] De lo anterior se obtiene que, \[ P \left( A \cap B \right)=\frac{n\left(A \cap B \right)}{n\left(S \right)}=\frac{2}{36} \; y \; P \left( B \right)=\frac{n\left( B \right)}{n\left(S \right)}=\frac{5}{36}. \] Luego, sustituyendo el resultado anterior en la ecuación (2.18) se obtiene que la probabilidad de que uno de los dados sea 2 si la suma es 6 es: \[ P \left( A \mid B \right)=\frac{P \left( A \cap B \right)}{P \left( B \right)}=\frac{\frac{2}{36}}{\frac{5}{36}}=\frac{2}{5}=0,4. \]

El espacio muestral \(S\) para este ejemplo se puede listar con el siguiente script de R. Note que en la tabla 2.1 las filas en color azul representa el evento \(A \cap B\).

dados <- urnsamples(
  1:6,
  size = 2, replace = TRUE,
  ordered = TRUE
) %>%
  as_tibble() %>%
  mutate(
    suma = X1 + X2
  )
kableExtra::kbl(
  dados,
  col.names = c("Dado 1", "Dado 2", "Suma"),
  format.args = list(decimal.mark = ",", big.mark = "."),
  booktabs = TRUE,
  caption = "\\label{tab2:dados}Lanzamiento de dos dados",
  escape = FALSE
) %>%
  kable_styling(
    bootstrap_options = "striped",
    full_width = FALSE,
    fixed_thead = TRUE
  ) %>%
  row_spec(
    which(
      dados$suma == "6" & (dados$X1 == "2" | dados$X2 == "2")
    ),
    color = "white", strikeout = FALSE, background = 'lightblue'
  ) %>%
  kable_classic_2() %>%
  scroll_box(width = "100%", height = "400px")

Tabla 2.1: Lanzamiento de dos dados

Dado 1	Dado 2	Suma
1	1	2
2	1	3
3	1	4
4	1	5
5	1	6
6	1	7
1	2	3
2	2	4
3	2	5
4	2	6
5	2	7
6	2	8
1	3	4
2	3	5
3	3	6
4	3	7
5	3	8
6	3	9
1	4	5
2	4	6
3	4	7
4	4	8
5	4	9
6	4	10
1	5	6
2	5	7
3	5	8
4	5	9
5	5	10
6	5	11
1	6	7
2	6	8
3	6	9
4	6	10
5	6	11
6	6	12

<br>

2.3.4.6 Teorema de la Multiplicación

Teorema 2.9 (Teorema de la Multiplicación para Dos Eventos) Si \(A\) y \(B\) son dos eventos cualesquiera de un espacio muestral \(S\) y \(P\left(A \right) \neq 0\), entonces \[ \begin{equation} P\left(A \cap B \right)=P \left(A \right) \cdot P \left( B \mid A \right). \tag{2.20} \end{equation} \]

En forma alternativa, si \(P\left(B \right) \neq 0\), entonces \[ \begin{equation} P\left(A \cap B \right)=P \left(B \right) \cdot P \left( A \mid B \right). \tag{2.21} \end{equation} \]

Teorema 2.10 (Teorema de la Multiplicación para Tres Eventos) Si \(A\), \(B\) y \(C\) son tres eventos cualesquiera de un espacio muestral \(S\), tal que \(P\left(A \cap B \right) \neq 0\), entonces \[ \begin{equation} P\left(A \cap B \cap C \right)=P \left(A \right) \cdot P \left( B \mid A \right) \cdot P \left( C \mid A \cap B \right). \tag{2.22} \end{equation} \]

Demostración. Al escribir \(A \cap B \cap C\) como \(\left(A \cap B \right) \cap C\) y utilizando la fórmula del teorema 2.9 dos veces, se obtiene \[ \begin{align*} P \left(A \cap B \cap C \right) & = P \left[ \left(A \cap B \right) \cap C \right] \\ & = P \left(A \cap B \right) \cdot P \left(C \mid A \cap B \right) \\ & = P \left(A \right) \cdot P \left( B \mid A \right) \cdot P \left( C \mid A \cap B \right). \end{align*} \]

Teorema 2.11 (Teorema de la Multiplicación para \(k\) Eventos) Si \(A{}_1, A{}_2, \dotsc, A{}_k\) son \(k\) eventos cualesquiera de un espacio muestral \(S\), tal que \(P\left(A{}_1 \cap A{}_2 \cap \cdots \cap A{}_{k-1} \right) \neq 0\) , entonces \[ \begin{align*} P\left(A_1 \cap A_2 \cap \cdots \cap A_k \right) = & P \left(A_1 \right) \cdot P \left( A_2 \mid A_1 \right) \cdot P \left( A_3 \mid A_1 \cap A_2 \right)\\ & \cdots P \left( A_k \mid A_1 \cap A_2 \cap \cdots \cap A_{k-1} \right). \tag{2.23} \end{align*} \]

Ejemplo 2.20 (Teorema de la Multiplicación para Dos Eventos) Determine la probabilidad de tomar de manera aleatoria o al azar en sucesión dos ases de un un mazo de cartas españolas a) si las cartas se toman sin reemplazo y b) si las cartas se toman con reemplazo.

1. Si \(A\) es el evento de que la primera carta es un as y \(B\) el evento de que la segunda carta es otro as. Entonces, la probabilidad de que las dos cartas sean ases, si el muestreo se realiza sin reemplazo, viene dado por \[ P\left(A \cap B \right)=P \left(A \right) \cdot P \left( B \mid A \right)=\frac{4}{40} \cdot \frac{3}{39}=\frac{1}{130}\approx 0,0077. \]

2. Si el muestreo se realiza con reemplazo la probabilidad de seleccionar dos ases es, \[ P\left(A \cap B \right)=P \left(A \right) \cdot P \left( B \mid A \right)=\frac{4}{40} \cdot \frac{4}{40}=\frac{1}{100}=0,01. \]

Ejemplo 2.21 (Teorema de la Multiplicación para Tres Eventos) Una caja de bombillos contiene 100 unidades, de los cuales 5 están defectuosos. Si se seleccionan al azar tres bombillos y se sacan de la caja en sucesión sin reemplazo, ¿cuál es la probabilidad de que los tres bombillos sean defectuosos.

Sea \(A\) el evento de que el primer bombillo es defectuosos, \(B\) el evento de que el segundo bobillo es defectuosos y \(C\) el evento de que el tercer bombillo es defectuosos. Entonces, la probabilidad de que los tres bombillos sean defectuosos, según ecuación (2.22) dada en el teorema 2.10 es \[ \begin{align*} P\left(A \cap B \cap C \right) & = P \left(A \right) \cdot P \left( B \mid A \right) \cdot P \left( C \mid A \cap B \right) \\ &=\frac{5}{100} \cdot \frac{4}{99}\cdot \frac{3}{98}\\ &=\frac{1}{16.170} \approx 0,00006. \end{align*} \]

2.3.4.7 Eventos Independientes

En términos informales, se dice que dos eventos \(A\) y \(B\) son independientes si la ocurrencia de uno no afecta la ocurrencia del otro. Por ejemplo, si se lanzan dos monedas es de esperarse que la ocurrencia de un resultado en una moneda no afecte el resultado en la otra moneda. Del mismo modo, si se considera el inciso b) del ejemplo 2.20 se puede ver que la ocurrencia de un as en la primera carta no afecta la ocurrencia de un as en la segunda carta, en tal sentido los eventos \(A\) y \(B\) son independientes. En contraste con lo anterior, el inciso a) muestra que los eventos \(A\) y \(B\) son dependientes dado que la ocurrencia de un as en la primera carta \(\left(P\left(A \right)=4/40 \right)\) afecta la ocurrencia de un as en la segunda carta \(\left(P\left(B \right)=3/40 \right)\).

Simbólicamente, dos eventos \(A\) y \(B\) son independientes si \(P \left( A \mid B \right)=P \left( A \right)\) y \(P \left( B \mid A \right) = P \left(B \right)\) y puede demostrarse que una u otra de estas igualdades implican a la otra cuando existen las dos probabilidades condicionales, es decir, cuando ni \(P \left( A \right)\) ni \(P \left( B \right)\) es igual a cero.

Ahora bien, si se sustituye \(P \left(B \right)\) por \(P \left( B \mid A \right)\) en la formula del teorema 2.9 se obtiene \[ \begin{align*} P\left(A \cap B\right) & =P\left(A \right) \cdot P \left( B \mid A \right)\\ & = P\left(A \right) \cdot P\left(B \right). \end{align*} \] De manera análoga, \[ \begin{align*} P\left(A \cap B\right) = P\left(B \cap A \right)& =P\left(B \right) \cdot P \left(A \mid B \right)\\ & = P\left(B \right) \cdot P \left(A \right)\\ & = P\left(A \right) \cdot P \left(B \right). \end{align*} \] De donde se concluye que los eventos \(A\) y \(B\) son independientes si \[ P\left(A \cap B \right)=P \left(A \right) \cdot P \left( B \right). \]

Definición 2.36 (Independencia de Dos Eventos) Dos eventos \(A\) y \(B\) cualesquiera de un espacio muestral \(S\) son independientes si y sólo si \[ \begin{equation} P\left(A \cap B \right)=P \left(A \right) \cdot P \left( B \right). \tag{2.24} \end{equation} \] De lo contrario, es decir, si \[ P\left(A \cap B \right) \neq P \left(A \right) \cdot P \left( B \right), \] se dice que los eventos \(A\) y \(B\) son dependientes.

Definición 2.37 (Independencia de Tres Eventos) Tres eventos \(A\), \(B\) y \(C\) cualesquiera de un espacio muestral \(S\) son independientes si se cumplen las dos condiciones siguientes:

1. Son independientes por pares, es decir \[ \begin{align*} & P\left(A \cap B \right)=P \left(A \right) \cdot P \left(B \right)\\ & P\left(A \cap C \right)=P \left(A \right) \cdot P \left(C \right)\\ & P\left(B \cap C \right)=P \left(B \right) \cdot P \left(C \right). \tag{2.25} \end{align*} \]
2. La probabilidad de la intersección de los tres eventos es igual a el producto de sus probabilidades, es decir
   \[ \begin{equation} P\left(A \cap B \cap C \right) =P \left(A \right) \cdot P \left(B \right) \cdot P \left(C \right) \tag{2.26} \end{equation} \]

Definición 2.37 (Independencia de \(k\) Eventos) Los eventos \(A{}_1, A{}_2, \dots, \;\textrm{y}\; A{}_k\) son independientes si y sólo si la probabilidad de la intersección de \(2, 3, \dots, \;\textrm{o}\; k\) de estos eventos es igual al producto de sus respectivas probabilidades. Es decir, \[ \begin{equation} P\left ( \bigcap_{i=i}^{k} A_i \right ) = P\left ( A_1 \right ) \, P\left ( A_2 \right ) \, \cdots \, P\left ( A_k \right ) \tag{2.27} \end{equation} \]

Teorema 2.12 Si los eventos \(A\) y \(B\) son independientes, entonces también lo son: \(a)\; A \;\textrm{y}\; B^c\), \(b)\; A^c \;\textrm{y}\; B\), \(c)\; A^c \;\textrm{y}\; B^c\). Es decir, \[ \begin{align*} a)\: & P \left( A \cap B^{c} \right) = P \left( A \right) \cdot P \left( B^{c} \right)\\ b)\: & P \left( A^{c} \cap B \right) = P \left( A^c \right) \cdot P \left( B \right)\\ c)\: & P\left( A^{c} \cap B^{c} \right) = P\left( A^{c} \right)\cdot P \left( B^{c} \right ). \tag{2.28} \end{align*} \]

Demostración. Como \(A=\left(A \cap B \right) \cup \left(A \cap B^c \right)\) y \(A \cap B\) y \(A \cap B^c\) son mutuamente excluyentes, se tiene que \[ \begin{align*} P\left(A \right) & = P\left[ \left(A \cap B \right) \cup \left(A \cap B^c \right) \right]\\ & = P \left(A \cap B \right) + P \left(A \cap B^c \right). \end{align*} \] Por otro lado, como \(A\) y \(B\) son independientes, \[ P\left(A \right)=P\left(A \right) \cdot P\left(B \right) + P \left(A \cap B^c \right). \] Despejando \(P \left(A \cap B^c \right)\) de la ecuación anterior, se obtiene que \[ \begin{align*} P \left(A \cap B^c \right) & = P\left(A \right) - P\left(A \right) \cdot P\left(B \right)\\ & = P\left(A \right) \cdot \left[1- P\left(B \right) \right]\\ & = P\left(A \right) \cdot P\left(B^c \right) \end{align*} \] y, por tanto, \(A\) y \(B^c\) son independientes.

Con respecto al inciso \(b)\), \(B=\left(A \cap B \right) \cup \left(A^c \cap B \right)\), Además, como \(A \cap B\) y \(A^c \cap B\) son mutuamente excluyentes, se tiene que \[ \begin{align*} P\left(B \right) & = P\left[ \left(A \cap B \right) \cup \left(A^c \cap B\right) \right]\\ & = P \left(A \cap B \right) + P \left(A^c \cap B \right). \end{align*} \] Por otro lado, como \(A\) y \(B\) son independientes, \[ P\left(B \right)=P\left(A \right) \cdot P\left(B \right) + P \left(A^c \cap B \right). \] Despejando \(P \left(A^c \cap B \right)\) de la ecuación anterior, se obtiene que \[ \begin{align*} P \left(A^c \cap B \right) & = P\left(A \right) - P\left(A \right) \cdot P\left(B \right)\\ & = P\left(B \right) \cdot \left[1- P\left(A \right) \right]\\ & = P\left(A^c \right) \cdot P\left(B \right) \end{align*} \] y, por tanto, \(A\) y \(B^c\) son independientes.

Con respecto al inciso \(c)\), por las leyes de Morgan 2.2.3.1 \(A^c \cap B^c=\left(A \cup B\right)^c\). Por tanto, \[ P\left ( A^{c} \cap B^{c} \right )=P \left[ \left(A \cup B\right)^c \right]. \] Luego, por la regla del complemento 2.5 \[ P\left ( A^{c} \cap B^{c} \right )=1-P\left ( A \cup B \right ). \] Por la regla de la unión de dos conjunto 2.7 \[ \begin{align*} P\left ( A^{c} \cap B^{c} \right )&=1-\left[P\left ( A \right )+P\left ( B \right )-P\left ( A \cap B \right ) \right]\\ &=1-P\left ( A \right )-P\left ( B \right )+P\left ( A \cap B \right ). \end{align*} \] Como \(A \;y\;B\) son independientes, entonces \[ P\left ( A^{c} \cap B^{c} \right )=1-P\left ( A \right )-P\left ( B \right )+P\left ( A \right ) \cdot P\left ( B \right ). \] Operando algebraicamente en el miembro derecho de la ecuación anterior se obtiene que \[ P\left ( A^{c} \cap B^{c} \right )=\left [ 1-P\left ( A \right ) \right ]\cdot \left [ 1-P\left ( B \right ) \right ]. \] Por último, por la regla del complemento 2.5, se obtiene que \[ P\left ( A^{c} \cap B^{c} \right )= P\left ( A^{c} \right )\cdot P\left ( B^{c} \right ). \] De donde se concluye que los eventos \(A^{c} \;\textrm{y}\; B^{c}\) son independientes si \(A \;\textrm{y}\; B\) lo son.

Ejemplo 2.22 (Eventos Independietes) Se lanzan tres monedas equilibradas las cueles pueden resultar en cara (\(c\)) o sello (\(s\)). Sean los eventos:

1. \(A: \{ \textrm{en las tres monedas sale el mismo signo} \}\),
2. \(B: \{ \textrm{por lo menos una de las tres monedas muestra cara} \}\) y
3. \(C: \{ \textrm{por lo menos salen dos caras} \}\).

Determine si estos eventos son independientes por pares.

De acuerdo a este experimento aleatorio, el espacio muestral \(S\) está determinado por, \[ S=\left\{ccc, ccs, csc, scc, ssc, scs, css, sss\right\}. \] Mientras que los eventos \(A\), \(B\), \(C\), \(A \cap B\), \(A \cap C\) y \(B \cap C\) viene dados por:

• \(A = \left\{ccc,sss\right\}\),
• \(B = \left\{ccc, scc, csc, ssc,ccs, scs, css\right\}\),
• \(C = \left\{ccc, scc, csc, ccs\right\}\),
• \(A \cap B= \left\{ccc\right\}\),
• \(A \cap C = \left\{ccc\right\}\) y
• \(B \cap C = \left\{ccc, scc, csc, ccs\right\}\),

respectivamente.

De lo anterior se obtiene que: \[ P \left(A \cap B \right)=\frac{1}{8} \neq P \left(A \right)\cdot P\left(B \right)=\frac{2}{8}\cdot\frac{7}{8}=\frac{7}{32}. \] De donde se deduce que los eventos \(A\) y \(B\) no son independientes, es decir, son dependientes.

Por otro lado, \[ P \left(A \cap C \right)=\frac{1}{8} = P \left(A \right)\cdot P\left(C \right)=\frac{2}{8}\cdot\frac{4}{8}=\frac{1}{8}. \] En consecuencia, los eventos \(A\) y \(C\) son independientes.

De manera análoga a como se procedió en los casos anteriores, \[ P \left(B \cap C \right)=\frac{4}{8}=\frac{1}{2} \neq P \left(B \right)\cdot P\left(C \right)=\frac{7}{8}\cdot\frac{4}{8}=\frac{7}{16}. \] Lo que implica que los eventos \(B\) y \(C\) no son independientes (son dependientes).

Note de la definición 2.37 que estos tres eventos no son independientes, dado que los eventos \(A\) y \(B\) y \(B\) y \(C\) no son independientes, aunque solo basta que uno de los tres pares de eventos no sean independientes para concluir que los tres eventos no son independientes.

2.3.4.8 Ley de la Probabilidad Total

Suponga que un espacio muestral \(S\) es la unión de los \(k\) eventos mutuamente excluyentes \(A{}_1, A{}_2, \dotsc, A{}_k\); es decir, \(A{}_1, A{}_2, \dotsc, A{}_k\) forman una partición de del conjunto \(S\). Además, suponga que \(E\) es cualquier subconjunto de \(S\). Entonces, como se ilustra en la figura 2.17 para el caso \(k=5\), \[ E=E \cap S=E \cap \left(A{}_1 \cup A{}_2 \cup \cdots \cup A{_k} \right)=\left(E \cap A{_1} \right) \cup \left(E \cap A{_2} \right) \cup \cdots \cup \left(E \cap A{_k} \right). \]

knitr::include_graphics(path = "figuras/probabilidad_total.png")

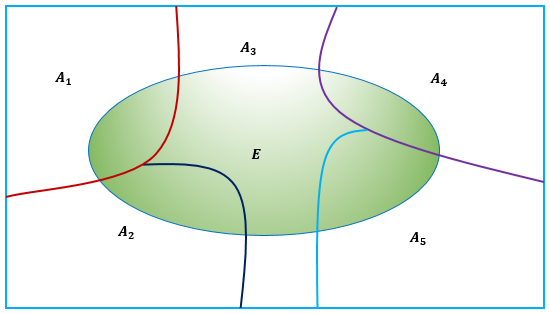
Figura 2.17: Diagrama de Ven para la probabilidad total

Como los \(k\) eventos a la derecha de la ecuación anterior son también mutuamente excluyentes, esta puede reescribirse de la siguiente manera (ver el axioma 3 de los axiomas de la probabilidad 2.3.4.4). \[ P \left(E \right)=P\left(E \cap A{_1} \right) + P\left(E \cap A{_2} \right) + \cdots + P\left(E \cap A{_k} \right). \] Luego, utilizando el teorema de multiplicación para dos eventos 2.9 en cada uno de los sumando de la ecuación anterior , bajo el supuesto de que \(P\left(A{}_i \right) \neq 0\) para \(i=1, 2, \dotsc, k\), se obtiene que \[ \begin{align*} P \left(E \right)&=P \left(A{}_1 \right) \cdot P \left( E \mid A{}_1 \right) + P \left(A{}_2 \right) \cdot P \left( E \mid A{}_2 \right) + \cdots + P \left(A{}_k \right) \cdot P \left( E \mid A{}_k \right)\\ &=\sum_{i=1}^{k}P\left ( A{}_i \right ) \cdot P\left ( E \mid A{}_i \right ) \end{align*} \] Lo anteriormente expuesto se resume en el siguiente teorema:

Teorema 2.13 (Ley de la Probabilidad Total) Sea \(E\) un evento en un espacio muestral \(S\) y sean los eventos \(A{}_1, A{}_2, \dotsc, A{}_k\) una partición de \(S\) para los cuales se cumple que \(P\left(A{}_i \right) \neq 0\) para \(i=1, 2, \dotsc, k\). Entonces, \[ \begin{equation} P \left(E \right)=\sum_{i=1}^{k}P\left ( A{}_i \right ) \cdot P\left ( E \mid A{}_i \right ). \tag{2.29} \end{equation} \]

Ejemplo 2.23 (Ley de la Probabilidad Total) Una fábrica utiliza tres máquinas \(A\), \(B\), \(C\) para producir ciertos artículos. Supongamos que:

1. La máquina \(A\) produce el 50% de todos los artículos, de los cuales el 3% son defectuosos.
2. La máquina \(B\) produce 30% de todos los artículos, de los cuales el 4% son defectuosos.
3. La máquina \(C\) produce 20% de todos los artículos, de los cuales el 5% son defectuosos.

Encuentre la probabilidad de que un artículo seleccionado aleatoriamente sea defectuoso.

knitr::include_graphics(
  path = "figuras/ejemplo1_probabilidad_total.png"
)

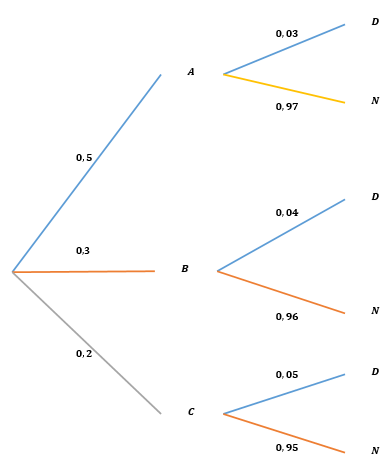
Figura 2.18: Diagrama de árbol del ejemplo 2.23

Sea el evento \(D: \{ \textrm{el artículo seleccionado es defectuoso} \}\) . Entonces, por la ley de la probabilidad total 2.13 y de acuerdo con la figura 2.18, se obtiene que \[ \begin{align*} P \left(D \right)&=P \left(A \right) \cdot P \left( D \mid A \right) + P \left(B \right) \cdot P \left( D \mid B \right) + P \left(C \right) \cdot P \left( D \mid C \right)\\ & = \left(0,5 \right) \cdot \left( 0,03 \right) + \left(0,3 \right) \cdot \left( 0,04 \right) + \left(0,2 \right) \cdot \left( 0,05 \right)\\ & =0,037=3,7\%. \end{align*} \]

2.3.4.9 Teorema de Bayes

Supóngase que los eventos \(A{}_1, A{}_2, \dotsc, A{}_k\) forman una partición del espacio muestral \(S\), y \(E\) es cualquier evento de \(S\). Entonces, para \(i=1, 2, \dotsc, k\), por definición de probabilidad condicional 2.35 \[ P \left( A{}_i \mid E \right)=\frac{P \left( A{}_i \cap E \right)}{P \left( E \right)}, \] si \(P\left(E \right) \neq 0\). Luego, aplicando el teorema de la multiplicación para dos eventos 2.9 en el numerador de la ecuación anterior se puede establecer que \[ P \left( A{}_i \mid E \right)=\frac{P \left( A_i \right) \cdot P \left( E \mid A_i \right)}{P \left( E \right)}, \] si \(P \left(A_i \right) \neq 0\) para \(i=1, 2, \dotsc, k\). Por último, haciendo uso de la ley de la probabilidad total 2.13 para el denominador en la ecuación anterior, se obtiene que \[ P \left( A{}_i \mid E \right)=\frac{P \left(A{}_i \right) \cdot P \left( E \mid A{}_i \right)}{\sum_{i=1}^{k}P\left ( A{}_i \right ) \cdot P\left ( E \mid A{}_i \right )}. \] El procedimiento anterior se resume en el siguiente teorema:

Teorema 2.14 (Teorema de Bayes) Si los eventos \(A{}_1, A{}_2, \dotsc, A{}_k\) constituyen una partición del espacio muestral \(S\) y \(P\left(A{}_i \right) \neq 0\) para \(i=1, 2, \dotsc, k\). Entonces, para un evento \(E\) cualquiera contenido en \(S\) tal que \(P\left(E \right) \neq 0\) \[ \begin{equation} P \left( A{}_i \mid E \right)=\frac{P \left(A{}_i \right) \cdot P \left( E \mid A{}_i \right)}{\sum_{i=1}^{k}P\left ( A{}_i \right ) \cdot P\left ( E \mid A{}_i \right )}, \textrm{para} i=1, 2, \dotsc, k. \tag{2.30} \end{equation} \]

Ejemplo 2.24 (Teorema de Bayes) Considere la fábrica en el ejemplo 2.23. Suponga que se ha encontrado un artículo defectuoso entre la producción. Encuentre la probabilidad de que este provenga de cada una de las máquinas, es decir, encuentre \(P \left( A \mid D \right)\), \(P \left( B \mid D \right)\) y \(P \left( C \mid D \right)\).

Como se mostró en el ejemplo 2.23 \[ \begin{align*} P \left(D \right)&=P \left(A \right) \cdot P \left( D \mid A \right) + P \left(B \right) \cdot P \left( D \mid B \right) + P \left(C \right) \cdot P \left( E \mid A{}_k \right)\\ & = \left(0,5 \right) \cdot \left( 0,03 \right) + \left(0,3 \right) \cdot \left( 0,04 \right) + \left(0,2 \right) \cdot \left( 0,05 \right)\\ & =0,037=3,7\%. \end{align*} \] Por tanto, aplicando el teorema de Bayes en el cálculo de las probabilidades requeridas se obtiene que:

• La probabilidad de que el artículo sea producido por la máquina \(A\) dado que está defectuoso se obtiene de la siguiente manera \[ P \left( A \mid D \right)=\frac{P \left(A \right) \cdot P \left( D \mid A \right)}{P\left ( D \right )}=\frac{ \left(0,5 \right) \cdot \left( 0,03 \right)}{\left ( 0,037 \right )}=\frac{15}{37}=40,5\%. \]
• La probabilidad de que el artículo sea producido por la máquina \(B\) dado que está defectuoso es \[ P \left( B \mid D \right)=\frac{P \left(B \right) \cdot P \left( D \mid B \right)}{P\left ( D \right )}=\frac{ \left(0,3 \right) \cdot \left( 0,04 \right)}{\left ( 0,037 \right )}=\frac{12}{37}=32,5\%. \]
• La probabilidad de que el artículo sea producido por la máquina \(C\) dado que está defectuoso viene dado por \[ P \left( C \mid D \right)=\frac{P \left(C \right) \cdot P \left( D \mid C \right)}{P\left ( D \right )}=\frac{ \left(0,2 \right) \cdot \left( 0,05 \right)}{\left ( 0,037 \right )}=\frac{10}{37}=27\%. \]

2.4 Información de Sesión

as_tibble(
  devtools::session_info()$packages
) %>%
  dplyr::select(
    package, loadedversion, source
  ) %>%
  dplyr::filter(
    package %in% packages
  ) %>%
  DT::datatable(
    rownames = FALSE,
    colnames = c(
      "Paquete", "Versión",
      "Fuente"
    ),
    caption = "Información de sesión",
    filter = "top",
    selection = "multiple",
    class = "cell-border stripe"
  )