Núcleo Temático 1 Técnicas de Conteo

En este núcleo temático se describen de manera teórica algunos métodos de conteo, tales como:

  1. Principio de la Adición (Sección 1.1)
  2. Principio de la Multiplicación (Sección 1.2)
    1. Diagrama de Árbol (Sección 1.2.1)
  3. Permutación (Sección 1.3)
    1. Permutación Sin Repetición (Sección 1.3.1)
    2. Permutación Con Repetición (Sección 1.3.2)
  4. Combinación (Sección 1.4)
    1. Combinación Sin Repetición (Sección 1.4.1)
    2. Combinación Con Repetición (Sección 1.4.2)
  5. Variación (Sección 1.5)
    1. Variación Sin Repetición (Sección 1.5.1)
    2. Variación Con Repetición (Sección 1.5.2)

Una vez descrita estas técnicas de conteo, se procede mediante ejemplos, a la implementación en R de las mismas.

El siguiente bloque de código permite instalar y cargar los paquetes usados para implementar estos métodos de conteo en R. De estos paquetes, los que contiene funciones relacionadas con la teoría de conteo son: combinat, gtools y prob.

packages <- c(
  "rmarkdown", "knitr", "knitcitations",
  "bookdown", "bookdownplus", "magrittr",
  "kableExtra", "DT", "devtools",
  "tidyverse", "htmltools", "htmlwidgets",
  "utf8", "stringr", "gtools", "prob",
  "combinat"
)
package.check <- lapply(packages, FUN = function(x) {
  if (!require(x, character.only = TRUE)) {
    install.packages(x, dependencies = TRUE)
    library(x, character.only = TRUE)
  }
})

1.1 Pricipio de la Adición

Definición 1.1 (Pricipio de la Adición) Si hay \(k\) procedimientos, tal que, el procedimiento 1 puede ocurrir de \(n_1\) manera, el procedimiento 2 puede ocurrir de \(n_2\) maneras, \(\dotsc\), y el procedimiento \(k\) puede ocurrir de \(n_k\) maneras. Entonces, el número de maneras \(n\) como podemos hacer el procedimiento 1, o el procedimiento 2, \(\dotsc\), o el procedimiento \(k\) es

\[ \begin{equation} n = n{}_1 + n{}_2 + \cdots + n{}_k. \tag{1.1} \end{equation} \] Suponiendo que los procedimientos no se pueden realizar en forma conjunta.

Ejemplo 1.1 (Pricipio de la Adición) Supongamos que planeamos un viaje y debemos decidir entre transportarnos por autobús, por avión o por tren. Si hay tres rutas para el autobús, dos para el avión y una para el tren, entonces hay \(n = n{}_1 + n{}_2 + n{}_3= 3 + 2 + 1 =6\) rutas disponibles para el viaje.

El resultado anterior puede conseguirse, mediante el siguiente script.

n1 <- 3
n2 <- 2
n3 <- 1
(nm <- n1 + n2 + n3)
#> [1] 6

Ejemplo 1.2 (Pricipio de la Adición) Suponga que en una biblioteca hay 3 novelas de misterio diferentes, 5 novelas de romance diferentes, 4 novelas de ficción diferentes y 2 novelas de aventura diferentes. Entonces hay

\[n = n_1 + n_2 + n_3 + n_4= 3 + 5 + 4 + 2 = 14\]

formas para escoger una de las novelas.

El siguiente fragmento de código, muestra el cálculo anterior.

n1 <- 3
n2 <- 5
n3 <- 4
n4 <- 2
(nm <- n1 + n2 + n3 + n4)
#> [1] 14

1.2 Principio de la Multiplicación

Definición 1.2 (Pricipio de la Multiplicación) Si hay \(k\) procedimientos, tal que, el procedimiento 1 se puede hacer de \(n_1\) manera, el procedimiento 2 se puede hacer de \(n_2\) maneras, \(\dotsc\), y el procedimiento \(k\) se puede hacer de \(n_k\) maneras. Entonces, el número de maneras \(n\) como podemos realizar el procedimiento 1, seguido del procedimiento 2, \(\dotsc\) , seguido del procedimiento \(k\) es

\[ \begin{equation} n = n{}_1\,n{}_2\cdots\,n{}_k. \tag{1.2} \end{equation} \]

Ejemplo 1.3 (Pricipio de la Multiplicación) Un artículo manufacturado debe pasar por tres controles. En cada uno de ellos se inspecciona una característica particular del artículo y se le marca de conformidad. En el primer control hay tres mediciones posibles, mientras que en cada uno de los últimos controles hay cuatro mediciones posibles. Por lo tanto, hay \(n = n_1 \, n_2 \, n_3= 3 · 4 · 4 = 48\) maneras de marcar el artículo.

En R, este resultado puede ser obtenido con el siguiente script.

n1 <- 3
n2 <- 4
n3 <- 4
(nm <- n1 * n2 * n3)
#> [1] 48

Ejemplo 1.4 (Pricipio de la Multiplicación) Juan va a armar una computadora por sí mismo. Tiene la opción de comprar los chips entre dos marcas, un disco duro de cuatro marcas, la memoria de tres marcas y un conjunto de accesorios en cinco tiendas locales. ¿De cuántas formas diferentes puede Juan armar la computadora?

Juan puede armar la computadora de \(n = n{}_1 \, n{}_2 \, n{}_3 \, n{}_4 = 2 \cdot 4 \cdot 3 \cdot 5 = 120\).

El siguiente trozo de código, muestra el resultado anterior.

n1 <- 2
n2 <- 4
n3 <- 3
n4 <- 5
(nm <- n1 * n2 * n3 * n4)
#> [1] 120

Ejemplo 1.5 (Pricipio de la Multiplicación) ¿Cuántos números pares de cuatro dígitos se pueden formar con los dígitos 0, 1, 2, 5, 6 y 9, si cada dígito se puede usar sólo una vez?

Como el número es par, tenemos sólo \(n_1 = 3\) elecciones para la posición de las unidades. Sin embargo, para un número de cuatro dígitos la posición de las unidades de mil no puede ser cero. Por lo tanto, consideramos la posición de las unidades en dos partes: 0 o diferentes de 0. Si la posición de las unidades es 0 (es decir, \(n_1 = 1\)), tenemos \(n_2 = 5\) elecciones para la posición de las unidades de mil, \(n_3 = 4\) para la posición de las centenas y \(n_4 = 3\) para la posición de las decenas. Por lo tanto, formamos un total de \[ n = n_1 \: n_2 \: n_3 \: n_4 = 1 \cdot 5 \cdot 4 \cdot 3 = 60 \] números pares de cuatro dígitos. Por otro lado, si la posición de las unidades no es 0 (es decir, \(n_1= 2\)), tenemos \(n_2 = 4\) elecciones para la posición de los unidades de mil, \(n_3 = 4\) para la posición de las centenas y \(n_4 = 3\) para la posición de las decenas. En esta situación tenemos un total de \[ n = n_1 \: n_2 \: n_3 \: n_4 = 2 \cdot 4 \cdot 4 \cdot 3 = 96 \] números pares de cuatro dígitos.

Como los dos casos no pueden ocurrir al mismo tiempo, por el principio aditivo, el número total de números pares de cuatro dígitos es \(60 + 96 = 156\).

El resultado anterior puede obtenerse en R con el siguiente bloque de código.

n11 <- 1
n12 <- 5
n13 <- 4
n14 <- 3
(nm1 <- n11 * n12 * n13 * n14)
n21 <- 2
n22 <- 4
n23 <- 4
n24 <- 3
(nm2 <- n21 * n22 * n23 * n24)
(nm <- nm1 + nm2)
#> [1] 60
#> [1] 96
#> [1] 156

1.2.1 Diagrama de Árbol

Definición 1.3 (Diagrama de Árbol) Un diagrama de árbol es un gráfico utilizado para enumerar todos los resultados posibles de una secuencia de procedimientos donde cada procedimiento puede ocurrir en un número finito de maneras. El diagrama de árbol se construye de izquierda a derecha y el número de ramas en cada punto corresponde al número de manera en que se puede realizar el procedimiento siguiente.

Ejemplo 1.6 (Diagrama de Árbol) Supóngase que un servicio de pruebas de productos evalúa el funcionamiento de una podadora de césped como fácil de operar, de dificultad mediana o difícil; como barata o cara; como de reparación barata, regular o costosa. ¿De cuántas maneras diferentes puede clasificarse una podadora de césped por dicho servicio?

Sea:

  • \(F_1\): la podadora de césped es fácil de operar
  • \(F_2\): la podadora de césped es medianamente fácil de operar
  • \(F_3\): la podadora de césped es difícil de operar
  • \(B_1\): la podadora de césped es barata
  • \(B_2\): la podadora de césped es cara
  • \(C_1\): la podadora de césped es barata de reparar
  • \(C_2\): la podadora de césped es de costo regular de reparación
  • \(C_3\): la podadora de césped es costosa de reparar

La figura 1.1 muestra el diagrama de árbol para las diferentes maneras en que se puede clasificar la podadora de césped.

knitr::include_graphics(path = "figuras/diagrama_arbol.png")
Diagrama de árbol para la clasificación de la podadora de césped

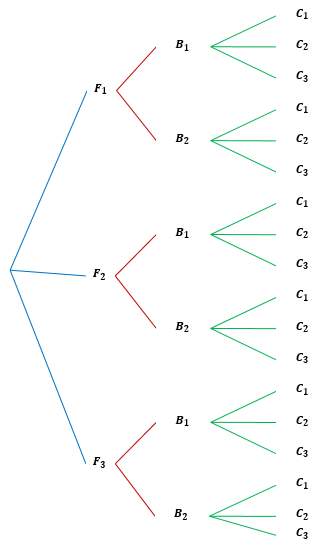
Figura 1.1: Diagrama de árbol para la clasificación de la podadora de césped

Ejemplo 1.7 (Diagrama de Árbol) Mario y Eduardo van a jugar un torneo de tenis. La primera persona que gane 2 juegos seguidos o quien gane un total de 3 juegos gana el torneo. Encuentre el número de formas como puede desarrollarse el torneo.

Dado que sólo hay dos resultados posibles en un encuentro de tenis entre estos dos jugadores, es decir: Mario gana el partido \(M\) ó Eduardo gana el partido \(E\). Los posibles resultados del torneo se indican en el diagrama de Venn mostrado en la figura 1.2.


knitr::include_graphics(path = "figuras/diagrama_arbol2.png")
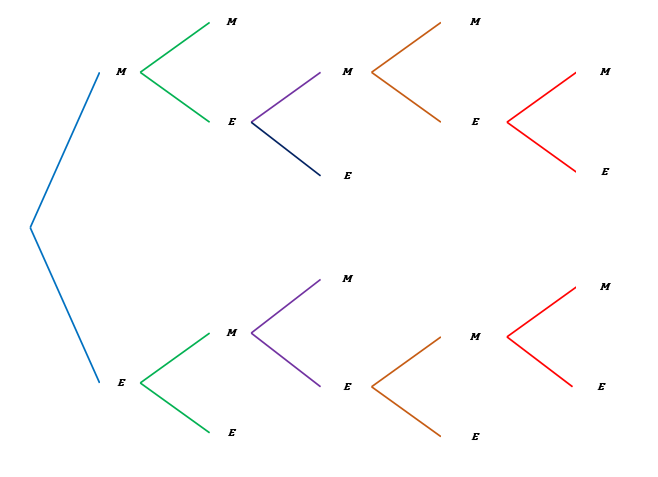
Diagrama de árbol para el número de formas como puede desarrollarse el torneo

Figura 1.2: Diagrama de árbol para el número de formas como puede desarrollarse el torneo

1.3 Permutación

Definición 1.4 (Permutación) Se define como cualquier arreglo, secuencias u ordenamiento de un conjunto de \(n\) objetos.

1.3.1 Permutación Sin Repetición

Definición 1.4 (Permutación Sin Repetición) Dados \(n\) objetos distintos, el número de permutaciones de éstos viene dado por: \[ \begin{equation} P_n=n!=n(n-1)(n-2)\cdots2\cdot1. \tag{1.3} \end{equation} \] Por definición \(0!=1\). \[3!=3\cdot2\cdot1=6\] \[5!=5\cdot4\cdot3\cdot2\cdot1=120\]

Ejemplo 1.8 (Permutación Sin Repetición) ¿Cuántas permutaciones se pueden hacer con las letras \(a\), \(b\) y \(c\)?

Los posibles casos son: \[ \begin{Bmatrix} (a,b,c);(a,c,b);(b,a,c);(b,c,a);(c,a,b);(c,b,a) \end{Bmatrix}. \] Usando la ecuación (1.3), el número de permutaciones sin repeticiones que se pueden obtener con las letras \(a\), \(b\) y \(c\) es \[ P_3=3\cdot2\cdot1=6. \] En R, este resultado se puede mostrar con el siguiente código. Note que en este bloque de código, el resultado anterior se ha calculado de dos manera, la primera, usando la función factorial de la distribución base de R, y la otra, usando la función nsamp del paquete prob.

factorial(3)
nsamp(n = 3, k = 3, replace = FALSE, ordered = TRUE)
#> [1] 6
#> [1] 6

La lista de premutaciones sin reemplazo se puede obtener con la función urnsamples del paquete prob.

urnsamples(
  c("a", "b", "c"),
  size = 3, replace = F,
  ordered = T
)
#>   X1 X2 X3
#> 1  a  b  c
#> 2  a  c  b
#> 3  c  a  b
#> 4  c  b  a
#> 5  b  c  a
#> 6  b  a  c

La función permutations del paquete gtools también lista estas permutaciones, como se muestra en el siguiente código.

gtools::permutations(
  n = 3, r = 3,
  v = c("a", "b", "c"), set = TRUE,
  repeats.allowed = FALSE
)
#>      [,1] [,2] [,3]
#> [1,] "a"  "b"  "c" 
#> [2,] "a"  "c"  "b" 
#> [3,] "b"  "a"  "c" 
#> [4,] "b"  "c"  "a" 
#> [5,] "c"  "a"  "b" 
#> [6,] "c"  "b"  "a"

Ejemplo 1.9 (Permutación Sin repetición) ¿Cuántas permutaciones se pueden hacer con las letras \(a\), \(b\), \(c\), \(d\)?

La lista de permutaciones sin repetición que se pueden obtener es: \[ \begin{Bmatrix} (a,b,c,d);&(a,b,d,c);&(a,c,b,d);&(a,c,d,b);&(a,d,b,c);\\(a,d,c,b);&(b,a,c,d);&(b,a,d,c);&(b,c,a,d);& (b,c,d,a);\\(b,d,a,c);&(b,d,c,a);&(c,a,b,d);&(c,a,d,b);&(c,b,a,d);\\(c,b,d,a);&(c,d,a,b);&(c,d,b,a);& (d,a,b,c);&(d,a,c,b);\\(d,b,a,c);&(d,b,c,a);&(d,c,a,b);&(d,c,b,a) \end{Bmatrix}. \]

Usando la ecuación (1.3), el número de permutaciones sin repeticiones que se pueden obtener con las letras \(a\), \(b\), \(c\) y \(d\) es: \[ P_4=4\cdot3\cdot2\cdot1=24. \]

El resultado anterior, se puede mostrar con el siguiente código. Aquí, como en el ejemplo 1.8, se han usado las funciones factorial y nsamp para determinar el número de permutaciones sin repetición.

factorial(4)
nsamp(n = 4, k = 4, replace = FALSE, ordered = TRUE)
#> [1] 24
#> [1] 24

La lista de permutaciones, en este caso, se muestra con el siguiente código.

urnsamples(c("a", "b", "c", "d"), size = 4, replace = F, ordered = T)
#>    X1 X2 X3 X4
#> 1   a  b  c  d
#> 2   a  b  d  c
#> 3   a  d  b  c
#> 4   d  a  b  c
#> 5   d  a  c  b
#> 6   a  d  c  b
#> 7   a  c  d  b
#> 8   a  c  b  d
#> 9   c  a  b  d
#> 10  c  a  d  b
#> 11  c  d  a  b
#> 12  d  c  a  b
#> 13  d  c  b  a
#> 14  c  d  b  a
#> 15  c  b  d  a
#> 16  c  b  a  d
#> 17  b  c  a  d
#> 18  b  c  d  a
#> 19  b  d  c  a
#> 20  d  b  c  a
#> 21  d  b  a  c
#> 22  b  d  a  c
#> 23  b  a  d  c
#> 24  b  a  c  d

Ejemplo 1.10 (Permutación Sin repetición) En una carrera de caballos en la cual participan 12. ¿De cuántas maneras pueden llegar los caballos a la meta, si no es posible que se den empates?

Usando la ecuación (1.3), el número de resultados posibles es: \[P_{12}=12!=12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1=479.001.600.\]

Usando R, este resultado puede obtenerse mediante el siguiente script.

factorial(12)
nsamp(
  n = 12, k = 12, replace = FALSE,
  ordered = TRUE
)
#> [1] 479001600
#> [1] 479001600

Abvertencia: La lista de posibles resultado de la carrera se puede generar con la instrucción urnsamples(1:12, size = 12, replace = F, ordered = T), pero no la ejecute porque la lista es muy grande y es posible que tarde mucho tiempo en generarse, además, consumiría mucho espacio en memoria.

1.3.2 Permutación Con Repetición

Definición 1.5 (Permutación Con Repetición) Dados \(n\) objetos, de los cuales \(n_1\) son de una clase, \(n_2\) de una segunda clase, \(\dotsc\) y \(n_k\) de una \(k\)-ésima clase; entonces el número de permutaciones distintas que se pueden formar con éstos \(n\) objetos viene dada por:

\[ \begin{equation} PR_{n}^{n_1, n_2, \dotsc, n_k}=\frac{n!}{n_1!\,n_2!\, \cdots \,n_k},\:con\: n=n_1+n_2+\cdots+n_k. \tag{1.4} \end{equation} \]

Este tipo de permutaciones también se conocen como Permutaciones de Objetos Indistinguibles.

Ejemplo 1.11 (Permutación Con repetición) Retomando el ejemplo 1.8, en el cual se calculó el número de permutaciones diferentes que se pueden formar con las letras \(a\), \(b\) y \(c\); supongamos que las letras \(b\) y \(c\) son iguales a \(x\), entonces los arreglos quedan definidos de la siguiente manera: \[ \begin{Bmatrix} (a,x,x); (a,x,x); (x,a,x); (x,x,a); (x,a,x); (x,x,a) \end{Bmatrix}. \]

Eliminando los casos idénticos, el número de permutaciones diferentes son: \[ \begin{Bmatrix} (a,x,x);(x,a,x);(x,x,a) \end{Bmatrix}. \] Usando la ecuación (1.4), el número de permutaciones con repeticiones en este caso será:

\[ PR_{3}^{1, 2}=\frac{3!}{1!\,2!}=3. \]

En R, este cálculo se consigue con la siguiente instrucción.

Pr <- factorial(3) / (factorial(1) * factorial(2))
paste("El número de permutaciones con repeticiones es ", Pr)
#> [1] "El número de permutaciones con repeticiones es  3"

La siguiente función facilita el cálculo de las permutaciones con repeticiones.

PR <- function(n, k) {
  if (n == sum(k)) {
    PR <- factorial(n) / prod(factorial(k))
  }
  else {
    PR <- "NAN"
  }
  return(PR)
}
paste(
  "El número de permutaciones con repeticiones es ", PR(n = 3, k = c(1, 2))
)
#> [1] "El número de permutaciones con repeticiones es  3"

La lista de premutaciones con repeticiones se puede obtener con el siguiente script. Note que el script lista todas las permutaciones sin repeticiones del vector c("a", "x", "x") y luego elimina las que se repiten.

urnsamples(
  x = c("a", "x", "x"), size = 3, replace = F,
  ordered = T
) %>%
  distinct()
#>   X1 X2 X3
#> 1  a  x  x
#> 2  x  a  x
#> 3  x  x  a

Ejemplo 1.12 (Permutación Con repetición) Ahora, retomando el ejemplo 1.9, donde calculamos el número de permutaciones diferentes que se pueden formar con las letras \(a\), \(b\), \(c\) y \(d\); supongamos que las letras \(a\), \(b\) son iguales a \(x\) y las letras \(c\) y \(d\) son iguales a \(y\). Es decir,

\[ \begin{Bmatrix} (x,x,y,y);&(x,x,y,y);&(x,y,x,y);&(x,y,x,y);&(x,y,x,y); \\(x,y,y,x);&(x,x,y,y);&(x,x,y,y);&(x,y,x,y);& (x,y,y,x); \\(x,y,x,y);&(x,y,y,x);&(y,x,x,y);&(y,x,y,x);&(y,x,x,y); \\(y,x,y,x);&(y,y,x,x);&(y,y,x,x);& (y,x,x,y);&(y,x,y,x); \\(y,x,x,y);&(y,x,y,x);&(y,y,x,x);&(y,y,x,x) \end{Bmatrix}. \]

Eliminando los casos que se repiten obtenemos el número de permutaciones diferentes, las cuales son:

\[ \begin{Bmatrix} (x,x,y,y); (x,y,x,y);(x,y,y,x);(y,x,x,y);(y,x,y,x);(y,y,x,x) \end{Bmatrix}. \]

Usando la ecuación (1.4), el número de permutaciones con repeticiones en este caso será:

\[ PR_{4}^{2, 2}=\frac{4!}{2!\,2!}=\frac{4(3)(2!)}{2!\,2!}=\frac{12}{2}=6. \]

El cálculo del número de permutaciones, en este ejemplo, se puede conseguir con el siguiente script.

paste(
  "El número de permutaciones con repeticiones es ", PR(n = 4, k = c(2, 2))
)
#> [1] "El número de permutaciones con repeticiones es  6"

La lista de premutaciones con repeticiones se puede obtener con el siguiente script. Note que el script lista todas las permutaciones sin repeticiones del vector c("x", "x", "y", "y") y luego elimina las que se repiten.

urnsamples(
  x = c("x", "x", "y", "y"),
  size = 4, replace = F, ordered = T
) %>%
  distinct()
#>   X1 X2 X3 X4
#> 1  x  x  y  y
#> 2  x  y  x  y
#> 3  y  x  x  y
#> 4  y  x  y  x
#> 5  x  y  y  x
#> 6  y  y  x  x

Ejemplo 1.13 (Permutación Con Repetición) Durante un entrenamiento del equipo de fútbol americano de la universidad, el coordinador defensivo necesita tener a 10 jugadores parados en una fila. Entre estos 10 jugadores, hay 1 de primer año, 2 de segundo año, 4 de tercer año y 3 de cuarto año, respectivamente. ¿De cuántas formas diferentes se pueden arreglar en una fila, si sólo se distingue su nivel de clase?

Si sólo se distingue su nivel de clase, la fila se puede arreglar de \[ PR_{10}^{1, 2, 4, 3}=\frac{10!}{1!\,2!\,4!\,3!}=\frac{10(9)(8)(7)(6)(5)(4!)}{2\,(4!)(6)}=12.600. \] maneras diferentes.

Con R, este resultado se puede mostrar con el siguiente bloque de código.

paste(
  "El número de permutaciones con repeticiones es ", formato(PR(n = 10, k = c(1, 2, 4, 3)))
)
#> [1] "El número de permutaciones con repeticiones es  12.600"

1.4 Combinación

Definición 1.6 (Combinación) Se define como cualquier selección de \(r\) objetos tomados de \(n\) objetos distintos, sin importar el orden.

1.4.1 Combinación Sin Repetición

Definición 1.7 (Conbinación Sin Repetición) Dados \(n\) objetos distintos, el número de combinaciones que se pueden formar con \(r\) de estos objetos viene dado por:

\[ \begin{equation} C_{n,r}=\binom{n}{r}=\frac{n!}{r!\left ( n-r \right )!}=\frac{n\left ( n-1 \right )\left ( n-2 \right )\,\cdots\,\left ( n-r+1 \right )}{r!}, con \,r\leq n. \tag{1.5} \end{equation} \]

Ejemplo 1.14 (Combinación Sin Repetición) Hay 12 estudiantes elegibles para asistir a la reunión anual de la Asociación Nacional de Estudiantes. Encuentre el número de formas como puede conformarse una delegación de 3 estudiantes, de los 12 estudiantes elegibles.

Esto se relaciona con combinación, no con permutaciones, puesto que el orden no cuenta en una delegación. En consecuencia, el número de formas en que puede formarse la delegación, según la ecuación (1.5) es:

\[ C_{12,3}=\binom{12}{3}=\frac{12!}{3!\left ( 12-3 \right )!}=\frac{12\left ( 11 \right )\left ( 10 \right )\left ( 9! \right )}{3!\left ( 9! \right )}=\frac{12\left ( 11 \right )\left ( 10 \right )}{3\left ( 2 \right )\left ( 1 \right )}=220. \]

La función nsamp del paquete prob, también ejecuta el cálculo anterior. Como se muestra en el siguiente bloque de código.

c1 <- nsamp(
  n = 12, k = 3, replace = FALSE,
  ordered = FALSE
)
paste("Se pueden formar", c1, "delegaciones")
#> [1] "Se pueden formar 220 delegaciones"

Ejemplo 1.15 (Conbinación Sin Repetición) ¿De cuántas maneras se pueden colocar dos anillos idénticos en la misma mano, de modo que no estén en el mismo dedo?

Los anillos se pueden colocar, según la ecuación (1.5), de

\[ C_{5,2}=\binom{5}{2}=\frac{5!}{2!\left ( 5-2 \right )!}=\frac{5\left ( 4 \right )\left ( 3! \right )}{2!\left ( 3! \right )}=\frac{5\left ( 4 \right )}{\left ( 2 \right )\left ( 1 \right )}=10 \] maneras.

Usando la función nsamp, al igual que en el ejemplo 1.14, el resultado anterior puede ser obtenido con el siguiente script.

c2 <- nsamp(
  n = 5, k = 2, replace = FALSE,
  ordered = FALSE
)
paste(
  "Los anillos se pueden colocar de", c2, "maneras"
)
#> [1] "Los anillos se pueden colocar de 10 maneras"

El siguiente script lista el número de maneras diferentes en que se pueden colocar los anillos en dos dedos diferentes de una mano.

prob::urnsamples(
  x = 1:5, size = 2, replace = FALSE,
  ordered = FALSE
)
#>    X1 X2
#> 1   1  2
#> 2   1  3
#> 3   1  4
#> 4   1  5
#> 5   2  3
#> 6   2  4
#> 7   2  5
#> 8   3  4
#> 9   3  5
#> 10  4  5

El resultado anterior, también se puede obtener con la función combinations del paquete gtools.

gtools::combinations(
  n = 5, r = 2, v = 1:5, set = TRUE,
  repeats.allowed = FALSE
)
#>       [,1] [,2]
#>  [1,]    1    2
#>  [2,]    1    3
#>  [3,]    1    4
#>  [4,]    1    5
#>  [5,]    2    3
#>  [6,]    2    4
#>  [7,]    2    5
#>  [8,]    3    4
#>  [9,]    3    5
#> [10,]    4    5

1.4.2 Combinación Con Repetición

Definición 1.8 (Combinación Con Repetición) Dados \(n\) objetos distintos, el número de combinaciones que se pueden formar con \(r\) de estos objetos, pudiendo haber objetos repetidos viene dado por:

\[ \begin{equation} CR_{n,r}=\binom{n+r-1}{n-1}=\binom{n+r-1}{r}=\frac{\left ( n+r-1 \right )!}{r!\left ( n-1 \right )!}=\frac{\left ( n+r-1 \right )\left ( n+r-2 \right )\cdots\left ( n+1 \right )n}{r!}. \tag{1.6} \end{equation} \]

Ejemplo 1.16 (Combinación Con Repetición) En un avión hay argentinos, peruanos, españoles y venezolanos. Se entrevista al azar a 10 de ellos. ¿De cuántas formas diferentes pueden resultar las nacionalidades?

En este ejemplo se tiene \(n=4\) nacionalidades distintas y se toma una muestra de \(r=10\) personas, note que en la muestra es posible que estén varios pasajeros de la misma nacionalidad.

De la ecuación (1.6), el número de formas diferentes en que puede resultar la nacionalidad es:

\[ CR_{4,10}=\binom{4+10-1}{4-1}=\binom{13}{3}=\frac{\left ( 13 \right )\left ( 12 \right )\left ( 11 \right )}{3!}=286. \]

La función nsamp del paquete prob, también ejecuta el cálculo anterior. Como se muestra en el siguiente bloque de código.

c1 <- nsamp(
  n = 4, k = 10, replace = TRUE,
  ordered = FALSE
)
paste(
  "Pueden resultar", c1, "nacionalidades distintas"
)
#> [1] "Pueden resultar 286 nacionalidades distintas"

Ejemplo 1.17 (Combinación Con Repetición) ¿Cuántas fichas tiene el juego del dominó?

Una ficha de dominó es un rectángulo en el que hay dos partes, en cada una de ellas hay una serie de puntos que indican la puntuación de esa parte. Estas puntuaciones van de blanca (0 puntos) a 6. Tenemos pares de puntuaciones de 0 a 6.

El total de fichas en el dominó, de acuerdo con la ecuación (1.6), serán:

\[ CR_{7,2}=\binom{7+2-1}{7-1}=\binom{8}{6}=\binom{8}{2}=\frac{\left ( 8 \right )\left ( 7 \right )}{2!}=28. \]

Haciendo uso de la función nsamp del paquete prob, el resultado anterior puede ser replicado con el siguiente script.

c1 <- nsamp(
  n = 7, k = 2, replace = TRUE,
  ordered = FALSE
)
paste(
  "El juego de dominó tiene", c1,
  "fichas distintas"
)
#> [1] "El juego de dominó tiene 28 fichas distintas"

Las piezas del dominó se pueden listar con el siguiente script.

combinations(
  n = 7, r = 2, v = 0:6, set = TRUE,
  repeats.allowed = TRUE
)
#>       [,1] [,2]
#>  [1,]    0    0
#>  [2,]    0    1
#>  [3,]    0    2
#>  [4,]    0    3
#>  [5,]    0    4
#>  [6,]    0    5
#>  [7,]    0    6
#>  [8,]    1    1
#>  [9,]    1    2
#> [10,]    1    3
#> [11,]    1    4
#> [12,]    1    5
#> [13,]    1    6
#> [14,]    2    2
#> [15,]    2    3
#> [16,]    2    4
#> [17,]    2    5
#> [18,]    2    6
#> [19,]    3    3
#> [20,]    3    4
#> [21,]    3    5
#> [22,]    3    6
#> [23,]    4    4
#> [24,]    4    5
#> [25,]    4    6
#> [26,]    5    5
#> [27,]    5    6
#> [28,]    6    6

Igual resultado se consigue con el siguiente fragmento de código.

urnsamples(
  x = 0:6, size = 2, replace = TRUE,
  ordered = FALSE
)
#>    X1 X2
#> 1   0  0
#> 2   0  1
#> 3   0  2
#> 4   0  3
#> 5   0  4
#> 6   0  5
#> 7   0  6
#> 8   1  1
#> 9   1  2
#> 10  1  3
#> 11  1  4
#> 12  1  5
#> 13  1  6
#> 14  2  2
#> 15  2  3
#> 16  2  4
#> 17  2  5
#> 18  2  6
#> 19  3  3
#> 20  3  4
#> 21  3  5
#> 22  3  6
#> 23  4  4
#> 24  4  5
#> 25  4  6
#> 26  5  5
#> 27  5  6
#> 28  6  6

1.5 Variación

Definición 1.9 (Variación) Se define como cualquier arreglo, secuencias u ordenación de \(r\) objetos tomados de \(n\) objetos.

1.5.1 Variación Sin Repetición

Definición 1.10 (Variación Sin Repetición) Dados \(n\) objetos diferente, el número de arreglos que se pueden formar con \(r\) de estos objetos viene dado por:

\[ \begin{equation} V_{n,r}=\frac{n!}{\left( n-r\right)!}=n\,(n-1)\,(n-2)\cdots(n-r+1),\:con\: r\leq n. \tag{1.7} \end{equation} \]

Ejemplo 1.18 (Variación Sin Repetición) En un año se otorgarán tres premios (a la investigación, la enseñanza y el servicio) en un grupo de 25 estudiantes de posgrado del departamento de estadística. Si cada estudiante puede recibir un premio como máximo, ¿cuántas selecciones posibles habría?

Como los premios son distinguibles, se trata de un problema de variación. Por lo tanto, aplicando la ecuación (1.7), el número total de posibilidades es

\[ V_{25,3}=\frac{25!}{\left( 25-3\right)!}=25\,(24)\,(23)=13.800. \] Con la función nsamp del paquete prob, este resultado se obtiene con el siguiente trozo de código.

c1 <- nsamp(
  n = 25, k = 3, replace = FALSE,
  ordered = TRUE
)
paste(
  "Se pueden hacer", formato(c1), "selecciones"
)
#> [1] "Se pueden hacer 13.800 selecciones"

Ejemplo 1.19 (Variación Sin Repetición) ¿De cuántas maneras se pueden colocar dos anillos diferentes en la misma mano, de modo que no estén en el mismo dedo?

Dado que los anillos son diferentes, en contraposición con el ejemplo 1.15, el orden en que se coloquen en los dedos hace diferencia, por lo tanto se trata de un caso de variación sin repetición. Por lo tanto, el número de formas diferentes en que se pueden colocar los anillos en dos dedos diferentes de la mano, según la ecuación (1.7) es:

\[ V_{5,2}=\frac{5!}{\left( 5-3\right)!}=\frac{5!}{ 2!}=5\,(4)=20. \] Este resultado, se puede obtener con el siguiente script.

c2 <- nsamp(
  n = 5, k = 2, replace = FALSE,
  ordered = TRUE
)
paste(
  "Los anillos se pueden colocar de",
  c2, "maneras"
)
#> [1] "Los anillos se pueden colocar de 20 maneras"

La lista de todas las posibles variaciones se puede obtener con el siguiente bloque de código.

urnsamples(
  x = 1:5, size = 2, replace = FALSE,
  ordered = TRUE
)
#>    X1 X2
#> 1   1  2
#> 2   2  1
#> 3   1  3
#> 4   3  1
#> 5   1  4
#> 6   4  1
#> 7   1  5
#> 8   5  1
#> 9   2  3
#> 10  3  2
#> 11  2  4
#> 12  4  2
#> 13  2  5
#> 14  5  2
#> 15  3  4
#> 16  4  3
#> 17  3  5
#> 18  5  3
#> 19  4  5
#> 20  5  4

El resultado anterior, también se puede obtener con la función permutations del paquete gtools.

permutations(
  n = 5, r = 2, v = 1:5, set = TRUE,
  repeats.allowed = FALSE
)
#>       [,1] [,2]
#>  [1,]    1    2
#>  [2,]    1    3
#>  [3,]    1    4
#>  [4,]    1    5
#>  [5,]    2    1
#>  [6,]    2    3
#>  [7,]    2    4
#>  [8,]    2    5
#>  [9,]    3    1
#> [10,]    3    2
#> [11,]    3    4
#> [12,]    3    5
#> [13,]    4    1
#> [14,]    4    2
#> [15,]    4    3
#> [16,]    4    5
#> [17,]    5    1
#> [18,]    5    2
#> [19,]    5    3
#> [20,]    5    4

1.5.2 Variación Con Repetición

Definición 1.11 (Variación Con Repetición) Dados \(n\) objetos diferentes, el número de arreglos que se pueden formar con \(r\) de estos objetos, pudiendo ocurrir que un mismo objeto aparezca más de una vez en el arreglo, viene dado por:

\[ \begin{equation} VR_{n,r}=n^r,\:con\: r\leq n. \tag{1.8} \end{equation} \]

Ejemplo 1.20 (Variación Con Repetición) ¿Cuántos arreglos se pueden formar con las letras \(a\), \(b\), \(c\) y \(d\); tomando dos de ellas y suponiendo que las letras se pueden repetir.

El número de arreglos posibles es el siguiente:

\[ \begin{Bmatrix} (a,a);&(a,b);&(a,c);&(a,d);\\(b,a);&(b,b);&(b,c);&(b,d);\\(c,a);&(c,b);&(c,c);&(c,d);\\(d,a);&(d,b) ;&(d,c);&(d,d) \end{Bmatrix}. \]

El número de arreglos diferentes que se pueden formar sin necesidad de listarlos, de acuerdo con la ecuación (1.8) es:

\[ VR_{4,2}=4^2=16. \]

La función nsamp del paquete prob ejecuta el cálculo anterior, por medio del siguiente bloque de código.

c1 <- nsamp(
  n = 4, k = 2, replace = TRUE,
  ordered = TRUE
)
paste(
  "Se pueden formar", formato(c1), "arreglos"
)
#> [1] "Se pueden formar 16 arreglos"

La lista de arreglos, usando R, se puede obtener con la siguiente instrucción.

urnsamples(
  x = c("a", "b", "c", "d"), size = 2,
  replace = TRUE, ordered = TRUE
)
#>    X1 X2
#> 1   a  a
#> 2   b  a
#> 3   c  a
#> 4   d  a
#> 5   a  b
#> 6   b  b
#> 7   c  b
#> 8   d  b
#> 9   a  c
#> 10  b  c
#> 11  c  c
#> 12  d  c
#> 13  a  d
#> 14  b  d
#> 15  c  d
#> 16  d  d

1.6 Ejercicios de Técnicas de Conteo

  1. Se va a despachar una flotilla de nueve taxis a tres aeropuertos, de modo que tres irán al aeropuerto A, cinco al aeropuerto B y uno al aeropuerto C. ¿De cuántas maneras distintas puede llevarse a cabo la tarea?

  2. ¿Cuántos números telefónicos distintos de siete dígitos pueden se pueden formar si el primero no puede ser cero?

  3. Un lujoso restaurante ofrece un menú especial o fixe prix, en el que por el precio de una comida puede elegir entre cuatro clases de aperitivos, tres de ensaladas, cuatro de guisados y cinco de postres. ¿Cuántos tipos de menú se ofrecen si cualquiera de ellos consta de aperitivo, ensalada, guisado y postre?

  4. Una mujer de negocios de Margarita desea prepara un itinerario para visitar seis ciudades importantes de Venezuela. La distancia del viaje y, por consiguiente, su costo depende del orden en que planifique su ruta. ¿Cuántos itinerarios diferentes (y costos de viaje) son posibles?

  5. Se llevó a cavo un estudio en la Universidad de Oriente Núcleo de Nueva Esparta para determinar la efectividad de cierta estrategia pedagógica. Para ello se tomó una muestra de 20 docentes de la institución. Si en la UDONE laboran 200 docentes.

    1. ¿Cuántas muestras diferentes pueden seleccionarse?
    2. Si de éstos 200 docentes el 40% son mujeres. ¿Cuántas muestras diferentes pueden obtenerse si el 40% de la muestra debe estar conformada por mujeres?

  6. Un grupo de amigos y amigas se encuentran y se dan un beso para saludarse. Si se han dado en total 21 besos. ¿Cuántas personas había?

  7. Lola tiene 25 bolitas (10 rojas, 8 azules y 7 blancas) para hacer un collar. Engarzando las 25 bolitas en un hilo, ¿cuántos collares distintos podrá realizar?

  8. Una fábrica de helados dispone de cinco sabores distintos (vainilla, chocolate, nata, fresa y cola) y quiere hacer helados de dos sabores. ¿cuántos tipos de helados podría fabricar?

  9. ¿De cuántas formas pueden cubrirse los cargos de presidente, vicepresidente, secretario y tesorero de un club deportivo sabiendo que hay 14 candidatos?

  10. En una carrera de 500 metros participan doce corredores. ¿De cuántas maneras pueden adjudicarse la medalla de oro, plata y bronce; suponiendo que no es posible de que ocurran empates?

  11. ¿Cuántas palabras distintas, con o sin sentido, podremos formar con las letras de la palabra educación? ¿y con la palabra vacaciones?

  12. ¿Cuántos números de seis cifras existen que estén formados por cuatro números dos y por dos números tres?

  13. ¿cuántos números de tres cifras se pueden formar con los dígitos 0, 1, 2, 3, 4, 5, 6 , 7, 8, 9 si ninguno se puede repetir?

  14. Con los números 1, 2, 3, 4, 5 y 6:

    1. ¿Cuántos números distintos de siete cifras podríamos formar?
    2. ¿Podremos numerar a los 3.224.564 habitantes de una ciudad con esos números?

1.7 Información de Sesión

as_tibble(devtools::session_info()$packages) %>%
  dplyr::select(
    package, loadedversion, source
  ) %>%
  dplyr::filter(
    package %in% packages
  ) %>%
  DT::datatable(
    rownames = FALSE,
    colnames = c(
      "Paquete", "Versión",
      "Fuente"
    ),
    caption = "Información de sesión",
    filter = "top",
    selection = "multiple",
    class = "cell-border stripe"
  )